In mathematics, a set A is Dedekind-infinite (named after the German mathematician Richard Dedekind) if some proper subset B of A is equinumerous to A...

choice is also true, then infinite sets are precisely the Dedekind-infinite sets. If an infinite set is a well-orderable set, then it has many well-orderings...

pronounce Dedekind. List of things named after Richard Dedekind Dedekind cut Dedekind domain Dedekind eta function Dedekind-infinite set Dedekind number...

Dedekind-infinite. The axiom of countable choice (ACω), a weak variant of the axiom of choice (AC), is needed to show that a set that is not Dedekind-infinite...

Dedekind–Hasse norm Dedekind-infinite set Dedekind–MacNeille completion Dedekind's axiom Dedekind's complementary module Dedekind lattice Jordan–Dedekind lattice...

contradictions within modern axiomatic set theory. Set theory as conceived by Georg Cantor assumes the existence of infinite sets. As this assumption cannot be...

the definition of an infinite set being any set that has a proper subset of the same cardinality (i.e., a Dedekind-infinite set); in this case {2,3,4...

to exist infinite Dedekind-finite sets that are not amorphous. No amorphous set can be linearly ordered. Because the image of an amorphous set is itself...

First Course in Noncommutative Rings. Springer Science & Business Media. ISBN 978-1-4684-0406-7. Dedekind-infinite set Von Neumann regular ring v t e...

cardinal to refer to the cardinality of a Dedekind-infinite set in contexts where this may not be equivalent to "infinite cardinal"; that is, in contexts where...

{\displaystyle \aleph _{0}} (namely, the cardinalities of Dedekind-finite infinite sets). Sets of these cardinalities satisfy the first three characterizations...

Dedekind-finite set is a set that is not Dedekind-infinite. (These are also spelled without the hyphen, as "Dedekind finite" and "Dedekind infinite"...

number) of the set. A set that is not a finite set is called an infinite set. For example, the set of all positive integers is infinite: { 1 , 2 , 3 ,...

uncountable sets, that is, sets that are not countable; for example the set of the real numbers. Although the terms "countable" and "countably infinite" as defined...

Blichfeldt's theorem Combinatorial principles Combinatorial proof Dedekind-infinite set Dirichlet's approximation theorem Hilbert's paradox of the Grand...

Cantor to Dedekind, the first dated July 28 and the second dated August 3. The role of the absolute infinite in Cantor's conception of set Infinity and...

mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized...

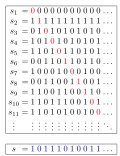
here is a proof (from ZF + ACω) that every infinite set is Dedekind-infinite: Let X {\displaystyle X} be infinite. For each natural number n {\displaystyle...

greater than the smallest infinite ordinal ω {\displaystyle \omega } , it follows that the consistency of second-order Zermelo set theory (and therefore also...

contains an ordered subfield that is isomorphic to the rational numbers. Any Dedekind-complete ordered field is isomorphic to the real numbers. The letters of...

as another, but that each line contains an infinite number. — Galileo, Two New Sciences Dedekind-infinite set Hilbert's paradox of the Grand Hotel MW Parker...

are more self-contained. In the Dedekind cut approach, each real number x {\displaystyle x} is defined as the infinite set of all rational numbers less than...

used sets of ordinals to produce an infinity of sets having different infinite cardinalities. His work on infinite sets together with Dedekind's set-theoretical...

B = {1, 2, 3, 4, 5, 6, 7}. A more elaborate example (involving two infinite sets) is: A = {x is an even integer larger than 1} B = {x is an odd integer...

are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers – informally, that there are sets which...

to prove it. In 1899, he sent Dedekind a proof of the equivalent aleph theorem: the cardinality of every infinite set is an aleph. First, he defined...

Secondly, both definitions involve infinite sets (Dedekind cuts and sets of the elements of a Cauchy sequence), and Cantor's set theory was published several...

In mathematics, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into...

infinity, which guarantees the existence of at least one infinite set, can be used to construct the set of natural numbers, N 0 {\displaystyle \mathbb {N} _{0}}...

implies the equivalence of infinite and Dedekind-infinite sets, but that the equivalence of infinite and Dedekind-infinite sets does not imply the axiom...