The Diffie–Hellman problem (DHP) is a mathematical problem first proposed by Whitfield Diffie and Martin Hellman in the context of cryptography and serves...

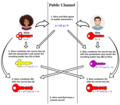
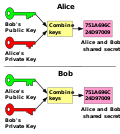
Diffie–Hellman (DH) key exchange is a mathematical method of securely generating a symmetric cryptographic key over a public channel and was one of the...

The decisional Diffie–Hellman (DDH) assumption is a computational hardness assumption about a certain problem involving discrete logarithms in cyclic groups...

complexity of the discrete logarithm problem, along with its application, was first proposed in the Diffie–Hellman problem. Several important algorithms in...

computational Diffie–Hellman (CDH) assumption is a computational hardness assumption about the Diffie–Hellman problem. The CDH assumption involves the problem of...

pioneers of public-key cryptography along with Martin Hellman and Ralph Merkle. Diffie and Hellman's 1976 paper New Directions in Cryptography introduced...

of the Decisional Diffie Hellman Problem in G {\displaystyle G} . The algorithm can be described as first performing a Diffie–Hellman key exchange to establish...

discrete logarithm problem (DLP), the computational Diffie–Hellman problem (CDH), and the computational co-Diffie–Hellman problem are all intractable...

Elliptic-curve Diffie–Hellman (ECDH) is a key agreement protocol that allows two parties, each having an elliptic-curve public–private key pair, to establish...

model assuming the intractability of the computational Diffie–Hellman problem in a gap Diffie–Hellman group. A signature scheme consists of three functions:...

and the truncated point problem. The decisional Diffie-Hellman problem is widely accepted as hard. The x-logarithm problem is not widely accepted as...

invention of public-key cryptography in cooperation with Whitfield Diffie and Ralph Merkle. Hellman is a longtime contributor to the computer privacy debate, and...

solved problem, particularly when the two users involved have never met and know nothing about each other. In 1976, Whitfield Diffie and Martin Hellman published...

Supersingular isogeny Diffie–Hellman key exchange (SIDH or SIKE) is an insecure proposal for a post-quantum cryptographic algorithm to establish a secret...

mathematical circles for originally identifying inadequacies in the "Diffie–Hellman problem", the basis for a large portion of modern network cryptography....

attacks. The security of the scheme is based on the computational Diffie–Hellman problem. Two variants of IES are specified: Discrete Logarithm Integrated...

generalizations of the computational Diffie–Hellman problem are believed to be infeasible while the simpler decisional Diffie–Hellman problem can be easily solved using...

them, under the assumption that a certain mathematical problem (e.g., the Diffie–Hellman problem in their proposal) is computationally infeasible (i.e...

cryptosystems, with different security goals, including digital signature, Diffie–Hellman key exchange, public-key key encapsulation, and public-key encryption...

can compute the shared secret, unless that party can solve the Diffie–Hellman problem. The public keys are either static (and trusted, say via a certificate)...

"hard" problems, often from number theory. For example, the hardness of RSA is related to the integer factorization problem, while Diffie–Hellman and DSA...

Logjam is a security vulnerability in systems that use Diffie–Hellman key exchange with the same prime number. It was discovered by a team of computer...

also possible to fight it off by working in groups with a hard Diffie–Hellman problem (DHP). Example: An attacker sees several outputs of the function...

P. (September 1998). "DHIES: An encryption scheme based on the Diffie-Hellman Problem (Appendix A)" (PDF). Rubin, K.; Silverberg, A. (2003). "Torus-Based...

work, he showed that the Diffie-Hellman problem is (under certain conditions) equivalent to solving the discrete log problem. From 2002 until 2008, Maurer...

secrecy typically uses an ephemeral Diffie–Hellman key exchange to prevent reading past traffic. The ephemeral Diffie–Hellman key exchange is often signed by...

field are the Diffie–Hellman-like key exchange CSIDH, which can serve as a straightforward quantum-resistant replacement for the Diffie–Hellman and elliptic...

scheme was described by Taher Elgamal in 1985. It is based on the Diffie–Hellman problem. The scheme involves four operations: key generation (which creates...

is infeasible (the computational Diffie–Hellman assumption): this is the "elliptic curve discrete logarithm problem" (ECDLP). The security of elliptic...

as well, including Diffie–Hellman key exchange and similar systems that depend on the security of the discrete logarithm problem rather than on integer...