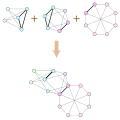
an edge contraction is an operation that removes an edge from a graph while simultaneously merging the two vertices that it previously joined. Edge contraction...

published in 1993. The idea of the algorithm is based on the concept of contraction of an edge ( u , v ) {\displaystyle (u,v)} in an undirected graph G = ( V ...

In computer science, the method of contraction hierarchies is a speed-up technique for finding the shortest path in a graph. The most intuitive applications...

speed up shortest-path routing Contraction mapping, a type of function on a metric space Edge contraction or vertex contraction, graph operations used in graph...

and k-edge-connected graphs (removing fewer than k edges cannot disconnect the graph). connected component Synonym for component. contraction Edge contraction...

operations, which create a new graph from an initial one, such as: edge contraction, line graph, dual graph, complement graph, graph rewriting; binary...

instruction—and performing an edge contraction for every edge that falsifies the predicate above, i.e. contracting every edge whose source has a single exit...

exists for every property of graphs that is preserved by deletions and edge contractions. For every fixed graph H, it is possible to test whether H is a minor...

graph obtained from G by edge contractions and vertex and edge deletions. The Hadwiger number is also known as the contraction clique number of G or the...

from the regular icosahedron, with one edge contraction, removing one vertex, 3 edges, and 2 faces. This contraction distorts the circumscribed sphere original...

are homeomorphic. The directed edges are shown to have an intermediate arrow head. Minor (graph theory) Edge contraction Archdeacon, Dan (1996), "Topological...

contraction operations by which they are formed correspond to edge deletion and edge contraction operations in graphs. The theory of matroid minors leads to...

recurrence relation called the deletion–contraction recurrence or Fundamental Reduction Theorem. It is based on edge contraction: for a pair of vertices u {\displaystyle...

(vertex identification); if the vertices are connected, this is called edge contraction. The condensation of a directed graph is the quotient graph where the...

as addition or deletion of a vertex or of an edge, merging and splitting of vertices, edge contraction, etc. The graph edit distance between a pair of...

between any two vertices in the same color class, thus the contraction is not an edge contraction (which is required for minors). Hadwiger's conjecture states...

graph by performing an edge contraction on every edge that is the only outgoing edge from its source and the only incoming edge into its target. Another...

i, no edge e ∈ C is selected for contraction, then Ci = C. Proof If G is not connected, then G can be partitioned into L and R without any edge between...

planar, so are all its minors: vertex and edge deletion obviously preserve planarity, and edge contraction can also be done in a planarity-preserving...

graph, f is a function on graphs, e is any edge of G, G \ e denotes edge deletion, and G / e denotes contraction. Tutte refers to such a function as a W-function...

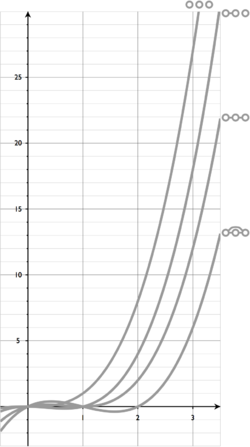
general case are unknown. A subcase of elementary collapse is edge-contraction. Edge contraction can be achieved in O ( k N l > j + C s D σ ) {\displaystyle...

and permutations, they observed that these operations correspond to edge contraction in a tree and its inverse. By applying a polynomial time dynamic programming...

It is a place where the cross section area is minimal. The maximum contraction takes place at a section slightly downstream of the orifice, where the...

{\displaystyle j} . A third definition uses a deletion–contraction recurrence. The edge contraction G / u v {\displaystyle G/uv} of graph G {\displaystyle...

formed from the original tree by edge contraction of all the heavy edges. A "light" edge of a given tree is an edge that was not selected as part of the...

into an edge (also creating a new edge), and edge contraction that eliminates vertices of degree two between edges (of the same color). Although such...

loop}}\\af(G/e)+bf(G\backslash e)&{\text{else}}\end{cases}}} Above G / e denotes edge contraction whereas G \ e denotes deletion. The numbers c, x, y, a, b are parameters...

parallelisations where the edges are simply divided between the cores. The main idea behind Borůvka's algorithm is edge contraction. An edge { u , v } {\displaystyle...

Michael Fellows in 1988, motivated by the fact that it is closed under edge contraction and induced subgraph operations. A polygon-circle graph can be represented...

Karger–Stein algorithm for finding minimum cuts in graphs, using a recursive edge contraction process. This algorithm calls itself twice recursively, with each call...