the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial can be...
19 KB (2,911 words) - 11:02, 4 April 2025
in terms of elementary symmetric polynomials. This implies that every symmetric polynomial expression in the roots of a monic polynomial can alternatively...
21 KB (3,833 words) - 19:46, 29 March 2025
algebraic combinatorics, the ring of symmetric functions is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
27 KB (3,850 words) - 18:08, 27 February 2024
elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of polynomial irreducible...
20 KB (3,773 words) - 12:22, 22 April 2025
polynomial expression in complete homogeneous symmetric polynomials. The complete homogeneous symmetric polynomial of degree k in n variables X1, ..., Xn, written...
15 KB (3,192 words) - 19:43, 28 January 2025
Newton's identities (redirect from Newton's theorem on symmetric polynomials)
types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monic polynomial P in one...
35 KB (7,650 words) - 23:11, 16 April 2025
Symmetry in mathematics (section Symmetric polynomials)
fundamental symmetric polynomials. A theorem states that any symmetric polynomial can be expressed in terms of elementary symmetric polynomials, which implies...
21 KB (2,837 words) - 17:16, 5 January 2025
Aside from polynomial functions, tensors that act as functions of several vectors can be symmetric, and in fact the space of symmetric k {\displaystyle...
5 KB (873 words) - 01:02, 18 December 2023
power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational...
6 KB (1,180 words) - 17:03, 10 April 2025
Newton's inequalities (redirect from Elementary symmetric mean)
{\displaystyle e_{k}} denote the kth elementary symmetric polynomial in a1, a2, ..., an. Then the elementary symmetric means, given by S k = e k ( n k )...
2 KB (252 words) - 21:14, 14 April 2025
Chern class (section Chern polynomial)
σk are elementary symmetric polynomials. In other words, thinking of ai as formal variables, ck "are" σk. A basic fact on symmetric polynomials is that...
42 KB (7,508 words) - 13:07, 21 April 2025
the i th elementary symmetric polynomial. The symmetric group Sn acts on the Xi by permuting them, and this induces an action on the polynomials in the...
9 KB (1,317 words) - 21:24, 21 February 2025
{1}{n^{2}}}={\frac {\pi ^{2}}{6}}.} Using formulae obtained from elementary symmetric polynomials, this same approach can be used to enumerate formulae for the...
44 KB (8,669 words) - 22:13, 22 June 2025
a_{2},\ldots ,a_{k-j+1}).} The elementary symmetric polynomial e n {\displaystyle e_{n}} and the power sum symmetric polynomial p n {\displaystyle p_{n}} can...
32 KB (7,647 words) - 15:09, 27 June 2025
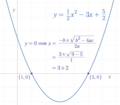
Quadratic formula (category Elementary algebra)
symmetric polynomials in α {\displaystyle \alpha } and β {\displaystyle \beta } . Specifically, they are the elementary symmetric polynomials –...
35 KB (5,787 words) - 19:29, 24 May 2025
Vieta's formulas (category Polynomials)
Gauss–Lucas theorem Properties of polynomial roots Rational root theorem Symmetric polynomial and elementary symmetric polynomial Ypma, Tjalling J. (1995). "Historical...
12 KB (2,587 words) - 10:40, 9 June 2025
Pieri's formula (category Symmetric functions)
the ring of symmetric functions, one obtains the dual Pieri rule for multiplying an elementary symmetric polynomial with a Schur polynomial: s μ e r =...
2 KB (242 words) - 08:56, 28 January 2024
Resultant (redirect from Polynomial resultant)
degree as elementary symmetric polynomial), then it is quasi-homogeneous of total weight de. If P and Q are homogeneous multivariate polynomials of respective...
46 KB (8,061 words) - 20:15, 4 June 2025
That is, it satisfies the condition A skew-symmetric ⟺ A T = − A . {\displaystyle A{\text{ skew-symmetric}}\quad \iff \quad A^{\textsf {T}}=-A.} In terms...
19 KB (3,632 words) - 21:44, 14 June 2025
, … {\displaystyle k=0,1,2,3,\ldots } ) be the kth-degree elementary symmetric polynomial in the variables x i = tan θ i {\displaystyle x_{i}=\tan...
83 KB (12,419 words) - 02:33, 25 June 2025
R_{F}} and its integral can be expressed as functions of the elementary symmetric polynomials in Δ x {\displaystyle \Delta x} , Δ y {\displaystyle \Delta...
14 KB (3,790 words) - 01:01, 11 May 2024
(Such a polynomial exists, because the expression is symmetric in the Xi and the elementary symmetric polynomials generate all symmetric polynomials.) Now...
12 KB (1,686 words) - 13:34, 28 May 2025
This issue doesn't arise when A is real and symmetric, resulting in a simple algorithm: % Given a real symmetric 3x3 matrix A, compute the eigenvalues % Note...
40 KB (4,870 words) - 04:25, 26 May 2025
Galois theory (redirect from Galois group of a polynomial)
originated in the study of symmetric functions – the coefficients of a monic polynomial are (up to sign) the elementary symmetric polynomials in the roots. For...
33 KB (4,221 words) - 15:58, 21 June 2025
For the remainder of this article, "symmetric group" will mean a symmetric group on a finite set. The symmetric group is important to diverse areas of...
46 KB (6,212 words) - 00:39, 20 June 2025
relation over Q {\displaystyle \mathbb {Q} } by using the fact that a symmetric polynomial whose arguments are all conjugates of one another gives a rational...
28 KB (4,778 words) - 00:16, 18 April 2025
Discriminant (redirect from Discriminant of a polynomial)
every polynomial which is homogeneous and symmetric in the roots may be expressed as a quasi-homogeneous polynomial in the elementary symmetric functions...
41 KB (6,704 words) - 20:17, 23 June 2025
Newton's theorem that every symmetric polynomial is a polynomial in the elementary symmetric polynomials, from polynomials to smooth functions. Glaeser...
955 bytes (83 words) - 08:08, 10 September 2020
are simpler in the case of monic polynomials: The ith elementary symmetric function of the roots of a monic polynomial of degree n equals ( − 1 ) i c n...
7 KB (1,159 words) - 12:21, 13 October 2023
Maclaurin's inequality (category Symmetric functions)
{n \choose k}}}.} The numerator of this fraction is the elementary symmetric polynomial of degree k {\displaystyle k} in the n {\displaystyle n} variables...
2 KB (501 words) - 21:13, 14 April 2025