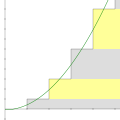
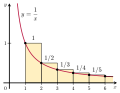
In mathematics, the Euler–Maclaurin formula is a formula for the difference between an integral and a closely related sum. It can be used to approximate...

Riemann zeta function. Euler–Maclaurin formula (Euler's summation formula) relating integrals to sums Euler–Rodrigues formula describing the rotation...

same methods, Maclaurin discovered the Euler–Maclaurin formula. He used it to sum powers of arithmetic progressions, derive Stirling's formula, and to derive...

{d}}x=n\ln n-n+1,} and the error in this approximation is given by the Euler–Maclaurin formula: ln ⁡ ( n ! ) − 1 2 ln ⁡ n = 1 2 ln ⁡ 1 + ln ⁡ 2 + ln ⁡ 3 + ⋯ +...

Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric...

functions, in Faulhaber's formula for the sum of m-th powers of the first n positive integers, in the Euler–Maclaurin formula, and in expressions for certain...

Infinite Summations Markus Mueller, Dierk Schleicher. Fractional Sums and Euler-like Identities S. P. Polyakov. Indefinite summation of rational functions...

Euler's Proof That 1 + 2 + 3 + ⋯ = −1/12 – by John Baez John Baez (September 19, 2008). "My Favorite Numbers: 24" (PDF). The Euler-Maclaurin formula,...

the Euler approximations. The most notable of these approximations are Euler's method and the Euler–Maclaurin formula. Euler helped develop the Euler–Bernoulli...

(mathematics) Direct comparison test Dominated convergence theorem Euler-Maclaurin formula Limit comparison test Monotone convergence theorem Knopp, Konrad...

be written by using sigma notation, as in the right side formula. With a = 0, the Maclaurin series takes the form: f ( 0 ) + f ′ ( 0 ) 1 ! x + f ″ ( 0...

theorem Vector Calculus Infinite series Maclaurin series, Taylor series Fourier series Euler–Maclaurin formula Adequality Infinitesimal Archimedes' use...

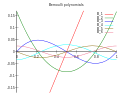
They are used for series expansion of functions, and with the Euler–MacLaurin formula. These polynomials occur in the study of many special functions...

are now known as the Euler approximations. The most notable of these approximations are Euler method and the Euler–Maclaurin formula. He also facilitated...

algorithm, in use prior to about 1930, proceeds by applying the Euler-Maclaurin formula to obtain, for n and m positive integers, ζ ( s ) = ∑ j = 1 n −...

extrapolation or the Euler–Maclaurin formula. This series can also be transformed into an integral by means of the Abel–Plana formula and evaluated using...

summation functions as a property of partial sums. If we take the Euler–Maclaurin summation formula together with the correction rule using Bernoulli numbers...

infinite product similar to the Euler product but taken over closed geodesics rather than primes. The Selberg trace formula is the analogue for these functions...

{1}{2k}}} and the Euler–Maclaurin formula. Using alternating signs with only odd unit fractions produces a related series, the Leibniz formula for π ∑ n = 0...

value to divergent series used by Ramanujan and based on the Euler–Maclaurin summation formula. The Ramanujan sum of a series f(0) + f(1) + ... depends not...

120 + · · · Harmonic series Tao, Terence (April 10, 2010), The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic...

order Euler–Maclaurin rules by adding a difference of 3rd, 5th, and so on derivatives with coefficients, as defined by Euler–MacLaurin formula. For some...

Leonhard Euler writes to James Stirling describing the Euler–Maclaurin formula, providing a connection between integrals and calculus. Euler produces...

S(x)=e^{iaf(x)}} where ƒ is a smooth function, we could use the Euler–Maclaurin formula to convert the series into an integral, plus some corrections involving...

_{s=a-1}^{b}f(s)\ ds.} For more general approximations, see the Euler–Maclaurin formula. For summations in which the summand is given (or can be interpolated)...

avoid double-counting, equivalent to the trapezoidal rule or the Euler–Maclaurin formula). That is, we approximate the cosine-series integral by the type-I...

sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can invite confusion with Euler numbers, or with Euler's constant,...

curves with a small indentation on the left and right of 0. Euler–Maclaurin summation formula Euler–Boole summation Ramanujan summation Hermite, C. (1901)...

canonical partition function for a classical rigid rod. Using the Euler–Maclaurin formula an improved estimate can be found ζ rot = k B T B + 1 3 + 1 15...

accurate as z increases. The expansion can be found by applying the Euler–Maclaurin formula to the sum ∑ n = 1 ∞ ( 1 n − 1 z + n ) {\displaystyle \sum _{n=1}^{\infty...