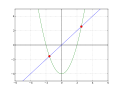
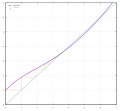
In mathematics, a fixed point (sometimes shortened to fixpoint), also known as an invariant point, is a value that does not change under a given transformation...

Fixed point may refer to: Fixed point (mathematics), a value that does not change under a given transformation Fixed-point arithmetic, a manner of doing...

In mathematics, a fixed-point theorem is a result saying that a function F will have at least one fixed point (a point x for which F(x) = x), under some...

In mathematics, a Hausdorff space X is called a fixed-point space if it obeys a fixed-point theorem, according to which every continuous function f : X...

point (mathematics), a point that is mapped to itself by the function Fixed line telephone, landline All pages with titles beginning with Fixed All pages...

In mathematics, Lawvere's fixed-point theorem is an important result in category theory. It is a broad abstract generalization of many diagonal arguments...

In combinatory logic for computer science, a fixed-point combinator (or fixpoint combinator): p.26  is a higher-order function (i.e., a function which...

In mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space X...

Among hundreds of fixed-point theorems, Brouwer's is particularly well known, due in part to its use across numerous fields of mathematics. In its original...

In numerical analysis, fixed-point iteration is a method of computing fixed points of a function. More specifically, given a function f {\displaystyle...

In mathematics, the Banach fixed-point theorem (also known as the contraction mapping theorem or contractive mapping theorem or Banach–Caccioppoli theorem)...

In order theory, a branch of mathematics, the least fixed point (lfp or LFP, sometimes also smallest fixed point) of a function from a partially ordered...

In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where...

In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry...

In mathematics, a number of fixed-point theorems in infinite-dimensional spaces generalise the Brouwer fixed-point theorem. They have applications, for...

In functional analysis, a branch of mathematics, the Ryll-Nardzewski fixed-point theorem states that if E {\displaystyle E} is a normed vector space and...

In computing, fixed-point is a method of representing fractional (non-integer) numbers by storing a fixed number of digits of their fractional part. Dollar...

In discrete mathematics, a discrete fixed-point is a fixed-point for functions defined on finite sets, typically subsets of the integer grid Z n {\displaystyle...

In the mathematical areas of order and lattice theory, the Kleene fixed-point theorem, named after American mathematician Stephen Cole Kleene, states the...

of Mathematics. 5 (2): 311–319. doi:10.2140/pjm.1955.5.311. Cousot, Patrick; Cousot, Radhia (1979). "Constructive versions of tarski's fixed point theorems"...

A mathematical object X has the fixed-point property if every suitably well-behaved mapping from X to itself has a fixed point. The term is most commonly...

In mathematical logic, fixed-point logics are extensions of classical predicate logic that have been introduced to express recursion. Their development...

fixed points in a n-dimensional space. Mathematically, a rotation is a map. All rotations about a fixed point form a group under composition called the...

In mathematics, the Borel fixed-point theorem is a fixed-point theorem in algebraic geometry generalizing the Lie–Kolchin theorem. The result was proved...

The Schauder fixed-point theorem is an extension of the Brouwer fixed-point theorem to locally convex topological vector spaces, which may be of infinite...

In mathematics, the Caristi fixed-point theorem (also known as the Caristi–Kirk fixed-point theorem) generalizes the Banach fixed-point theorem for maps...

Fixed-point computation refers to the process of computing an exact or approximate fixed point of a given function. In its most common form, the given...

In mathematics, the Atiyah–Bott fixed-point theorem, proven by Michael Atiyah and Raoul Bott in the 1960s, is a general form of the Lefschetz fixed-point...

In mathematics, the common fixed point problem is the conjecture that, for any two continuous functions that map the unit interval into itself and commute...

In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation. The point x ~ ∈ R n {\displaystyle...