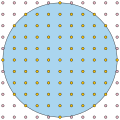
In mathematics, the Gauss circle problem is the problem of determining how many integer lattice points there are in a circle centered at the origin and...

Riemannian geometry Gauss map in differential geometry Gaussian curvature, defined in his Theorema egregium Gauss circle problem Gauss–Kuzmin–Wirsing constant...

Johann Carl Friedrich Gauss (/ɡaʊs/ ; German: Gauß [kaʁl ˈfʁiːdʁɪç ˈɡaʊs] ; Latin: Carolus Fridericus Gauss; 30 April 1777 – 23 February 1855) was a German...

Separation between two points Gauss circle problem – How many integer lattice points there are in a circle Inversion in a circle – Study of angle-preserving...

today, this problem remains unsolved. Progress has been slow. Many of the same methods work for this problem and for Gauss's circle problem, another lattice-point...

pair? The Gauss circle problem: how far can the number of integer points in a circle centered at the origin be from the area of the circle? Grand Riemann...

adjacent rays Five circles theorem – Derives a pentagram from five chained circles centered on a common sixth circle Gauss circle problem – How many integer...

a circular membrane Weber function (defined at Anger function) Gauss' circle problem Dutka, Jacques (1995). "On the early history of Bessel functions"...

grid points. The Gauss circle problem concerns bounding the error between the areas and numbers of grid points in circles. The problem of counting integer...

to some measure of "size" or height. An important example is the Gauss circle problem, which asks for integers points (x y) which satisfy x 2 + y 2 ≤ r...

theory. Most of the unsolved problems are related to distribution of Gaussian primes in the plane. Gauss's circle problem does not deal with the Gaussian...

the table below: Integer partition Jacobi's four-square theorem Gauss circle problem P. T. Bateman (1951). "On the Representation of a Number as the Sum...

let us mention two classical examples, Dirichlet's divisor problem and the Gauss circle problem. The former estimates the size of d(n), the number of positive...

According to Weierstrass in his paper, earlier mathematicians including Gauss had often assumed that such functions did not exist. It was conjectured...

the article on the Gauss circle problem, one can compute this by approximating the number of lattice points inside of a quarter circle centered at the origin...

attempted to square the circle and claim success—despite the fact that it is mathematically impossible. An unsolved problem thus far is the question...

the dies have a square aspect ratio, we arrive at the Gauss Circle Problem, an unsolved open problem in mathematics.) Note that formulas estimating the gross...

combinatorial optimization. The Gauss circle problem asks for the number of points of the integer lattice enclosed by a given circle. One of Jarník's theorems...

area enclosed by a circle of radius r is πr2. Here, the Greek letter π represents the constant ratio of the circumference of any circle to its diameter,...

Polygon Carlyle circle Bold, Benjamin. Famous Problems of Geometry and How to Solve Them, Dover Publications, 1982 (orig. 1969). Gauss, Carl Friedrich...

term. The Dirichlet divisor problem that estimates the average order of the divisor function d(n) and Gauss's circle problem that estimates the average...

Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga...

to do so. Gauss showed that some polygons are constructible but that most are not. Some of the most famous straightedge-and-compass problems were proved...

Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor. Mohr's circle is often used in calculations...

In mathematics, Kummer sum is the name given to certain cubic Gauss sums for a prime modulus p, with p congruent to 1 modulo 3. They are named after Ernst...

problem of trying to find the best visual fit of circle to a set of 2D data points. The method elegantly transforms the ordinarily non-linear problem...

proof of the conjecture, and the next step was taken by Carl Friedrich Gauss (1831), who proved that the Kepler conjecture is true if the spheres have...

problèmes de Géométrie-pratique [Little-known solutions of various Geometry practice problems] (in French). Devilly, Metz et Courcier. p. 15. Gauss,...

sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions (where the problem becomes circle packing in two dimensions...

the letter to Wolfgang (Farkas) Bolyai of March 6, 1832 Gauss claims to have worked on the problem for thirty or thirty-five years (Faber 1983, p. 162)....