A height function is a function that quantifies the complexity of mathematical objects. In Diophantine geometry, height functions quantify the size of...
17 KB (1,908 words) - 08:10, 5 April 2025
tree, the height of a vertex is the length of the longest downward path to a leaf from that vertex; In algebraic number theory, a "height function" is a measurement...
8 KB (1,037 words) - 20:39, 14 July 2025
mathematics, the height zeta function of an algebraic variety or more generally a subset of a variety encodes the distribution of points of given height. If S is...
2 KB (347 words) - 06:15, 29 March 2019
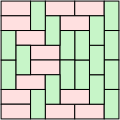
Domino tiling (section Height functions)
height function associating an integer to the vertices of the grid. For instance, draw a chessboard, fix a node A 0 {\displaystyle A_{0}} with height...
13 KB (1,509 words) - 01:15, 22 June 2025
properties of an element Height (ring theory), a measurement in commutative algebra Height (triangle) or altitude Height function, a function that quantifies the...
1 KB (206 words) - 05:51, 22 April 2024
Below are two tables which report the average adult human height by country or geographical region. With regard to the first table, original studies and...
166 KB (8,637 words) - 15:26, 19 July 2025
Glossary of arithmetic and diophantine geometry (redirect from Naive height)
Canonical height The canonical height on an abelian variety is a height function that is a distinguished quadratic form. See Néron–Tate height. Chabauty's...
37 KB (4,753 words) - 14:39, 23 July 2024
Gaussian random field, a central model of random surfaces (random height functions). The discrete version can be defined on any graph, usually a lattice...
10 KB (1,509 words) - 11:39, 4 July 2025
Automorphic form (redirect from Fuchsian function)
operators on G; and to satisfy a "moderate growth" asymptotic condition a height function. It is the first of these that makes F automorphic, that is, satisfy...
13 KB (1,652 words) - 04:27, 18 May 2025
This height function h has the property that h(mP) grows roughly like the square of m. Moreover, only finitely many rational points with height smaller...
54 KB (8,443 words) - 07:21, 30 July 2025
mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the...
76 KB (11,410 words) - 20:15, 22 May 2025
common, that they have a fluctuating height function or some analogue function, that can be thought of as a function, that models the growth of the model...
7 KB (1,268 words) - 08:46, 13 July 2024
Heights of presidents and presidential candidates of the United States (redirect from List of United States Presidents by height order)
candidates of the United States is useful for evaluating what role, if any, height plays in presidential elections in the United States. Some observers have...
67 KB (3,430 words) - 13:27, 1 August 2025
This requires the introduction of a height function on the set of rational elliptic curves. To define such a function, recall that a rational elliptic curve...
18 KB (2,799 words) - 21:23, 12 July 2025
[citation needed] Height finding radars of the 1960s and 70s were distinguished by their antenna being tall, but narrow. As beam shape is a function of antenna...
4 KB (416 words) - 21:39, 2 August 2024
similar formal properties to the abscissa of convergence of the height zeta function and it is conjectured that they are essentially the same. More precisely...
2 KB (305 words) - 16:42, 27 July 2023
_{2})\cdots (z-\alpha _{n}).} The Mahler measure can be viewed as a kind of height function. Using Jensen's formula, it can be proved that this measure is also...
15 KB (2,296 words) - 01:13, 30 March 2025
of rational points on an algebraic variety relative to a suitable height function. It was proposed by Yuri I. Manin and his collaborators in 1989 when...
3 KB (371 words) - 16:43, 24 March 2025
zeta function of a variety Height zeta function of a variety Hurwitz zeta function, a generalization of the Riemann zeta function Igusa zeta function Ihara...
3 KB (379 words) - 14:35, 7 September 2023
mathematical analysis, the Dirac delta function (or δ distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value...
98 KB (14,418 words) - 05:48, 22 July 2025
same basic structure. The second half of the proof needs some type of height function, in terms of which to bound the 'size' of points of A ( K ) {\displaystyle...
5 KB (619 words) - 18:23, 30 November 2024
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form f ( x ) = exp ( − x 2 ) {\displaystyle f(x)=\exp(-x^{2})}...
30 KB (5,023 words) - 17:40, 4 April 2025
headphone jack, four-speaker sound system with Spatial Audio, full height function keys, and four finishes (Silver, Space Gray, Starlight, and Midnight)...
48 KB (3,702 words) - 01:31, 29 July 2025
List of tallest buildings (redirect from List of tallest buildings by height to roof)
intended here as enclosed structures with continuously occupiable floors and a height of at least 350 metres (1,150 ft). Such definition excludes non-building...
96 KB (3,462 words) - 15:18, 30 July 2025
Gradient (section Linear approximation to a function)
scalar-valued differentiable function f {\displaystyle f} of several variables is the vector field (or vector-valued function) ∇ f {\displaystyle \nabla...
37 KB (5,689 words) - 18:55, 15 July 2025
Kangaroo (redirect from Kangaroo hopping height)
from humans: mice are too close and have not developed many different functions, while birds are genetically too remote. The dairy industry could also...
69 KB (7,549 words) - 05:42, 12 July 2025
28.964 Da × 1.660×10−27 kg/Da = 4.808×10−26 kg. As a function of temperature, the scale height of Earth's atmosphere is therefore H/T = kB/mg = 1.381×10−23 J⋅K−1...
15 KB (1,991 words) - 16:14, 14 June 2025
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined...
74 KB (10,595 words) - 18:29, 27 July 2025
example, the function H(t) denoting the height of a growing flower at time t would be considered continuous. In contrast, the function M(t) denoting...
63 KB (9,324 words) - 15:49, 8 July 2025
mathematicians Michael Prähofer and Herbert Spohn. They proved that the height function of a model from the (1+1)-dimensional KPZ universality class - the...
6 KB (953 words) - 11:39, 2 August 2025