analytic number theory, Mertens' theorems are three 1874 results related to the density of prime numbers proved by Franz Mertens. In the following, let...

For Mertens' results on the distribution of prime numbers, see Mertens' theorems. For Mertens' result on convergence of Cauchy products of series, see...

Franz Mertens (20 March 1840 – 5 March 1927) (also known as Franciszek Mertens) was a German-Polish mathematician. He was born in Schroda in the Grand...

(an)n≥0 and (bn)n≥0 be real or complex sequences. It was proved by Franz Mertens that, if the series ∑ n = 0 ∞ a n {\textstyle \sum _{n=0}^{\infty }a_{n}}...

theorems, and Meissel–Mertens constant Franz Carl Mertens (1764–1831), German botanist Gregory Mertens (1991–2015), Belgian footballer Helmut Mertens...

called a theorem is a proved result that is not an immediate consequence of other known theorems. Moreover, many authors qualify as theorems only the...

formulation of the Riemann hypothesis. The third of Mertens' theorems.* The calculation of the Meissel–Mertens constant. Lower bounds to specific prime gaps...

The Meissel–Mertens constant (named after Ernst Meissel and Franz Mertens), also referred to as the Mertens constant, Kronecker's constant (after Leopold...

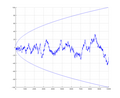
In mathematics, the Mertens conjecture is the statement that the Mertens function M ( n ) {\displaystyle M(n)} is bounded by ± n {\displaystyle \pm {\sqrt...

whether all admissible k-tuples have a corresponding Skewes number. Mertens' theorems § Changes in sign Kreisel (1951) quotes A. E. Ingham (1932) and J...

This is a list of notable theorems. Lists of theorems and similar statements include: List of algebras List of algorithms List of axioms List of conjectures...

confirmed by later mathematicians as one of Mertens' theorems, and can be seen as a precursor to the prime number theorem. Another problem in number theory closely...

^{h}x}}\right)\ .} The Mertens conjecture went further, stating that there would be no x where the absolute value of the Mertens function exceeds the square...

member, and getting the previous value before a member. Using one of Mertens' theorems (the third) it can be shown to use O(N / log log N) of these operations...

extrapolation Series acceleration Steffensen's method Hugh J. Hamilton, "Mertens' Theorem and Sequence Transformations", AMS (1947) Transformations of Integer...

theorem could be considered a weaker version of his own theorem[failed verification] and other utility representation theorems like the VNM theorem,...

of the first known proofs of theorems in geometry. Eudoxus (408–355 BCE) and Theaetetus (417–369 BCE) formulated theorems but did not prove them. Aristotle...

Jean-François Mertens (11 March 1946 – 17 July 2012) was a Belgian game theorist and mathematical economist. Mertens contributed to economic theory in...

9, pp. 160–188, Theorems 7 and 8. In Theorem 7 Euler proves the formula in the special case s = 1 {\displaystyle s=1} , and in Theorem 8 he proves it more...

super-prime 2093 – Mertens function zero 2095 – Mertens function zero 2096 – Mertens function zero 2097 – Mertens function zero 2099 – Mertens function zero...

of O'N as follows: In 2017 John F. R. Duncan, Michael H. Mertens, and Ken Ono proved theorems that establish an analogue of monstrous moonshine for the...

where it is also the fiftieth number to return 0 {\displaystyle 0} in the Mertens function. While the twenty-first prime number 73 is the largest member...

the United States. Franciszek Mertens, mathematician known for Mertens function, Mertens conjecture, Mertens's theorems. Josef Hofmann, designer of first...

M. B. (2005). "Mertens' Proof of Mertens' Theorem". arXiv:math/0504289. In respective order from Apostol's book: Exercise 2.29, Theorem 2.18, and Exercises...

by Elon Kohlberg and Jean-François Mertens for games with finite numbers of players and strategies. Later, Mertens proposed a stronger definition that...

while the second was published in 2020. Similar identities hold for the Mertens function. The formula ∑ d ∣ n μ ( d ) = { 1 if  n = 1 , 0 if  n > 1 {\displaystyle...

induction. To resolve the problem Jean-François Mertens introduced what game theorists now call Mertens-stable equilibrium concept, probably the first...

In combinatorial game theory, the Sprague–Grundy theorem states that every impartial game under the normal play convention is equivalent to a one-heap...

In game theory, folk theorems are a class of theorems describing an abundance of Nash equilibrium payoff profiles in repeated games (Friedman 1971). The...

(for example, the Paris–Harrington theorem) provable using second order but not first-order methods, but such theorems are rare to date. Erdős and Selberg's...