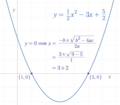
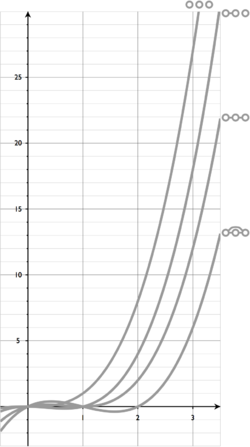
In algebra, a monic polynomial is a non-zero univariate polynomial (that is, a polynomial in a single variable) in which the leading coefficient (the...

integers. That is, an algebraic integer is a complex root of some monic polynomial (a polynomial whose leading coefficient is 1) whose coefficients are integers...

the ideal of polynomials vanishing on α. The minimal polynomial f of α is unique. To prove this, suppose that f and g are monic polynomials in Jα of minimal...

Monic or monic in Wiktionary, the free dictionary. Monic may refer to: Monic morphism, a special kind of morphism in category theory Monic polynomial...

to be a −∞. A constant polynomial is either the zero polynomial, or a polynomial of degree zero. A nonzero polynomial is monic if its leading coefficient...

non-constant monic polynomial with coefficients in F is irreducible over F, if it is not the product of two non-constant monic polynomials, with coefficients...

minimal polynomial μA of an n × n matrix A over a field F is the monic polynomial P over F of least degree such that P(A) = 0. Any other polynomial Q with...

roots of a monic polynomial can alternatively be given as a polynomial expression in the coefficients of the polynomial. Symmetric polynomials also form...

divide the quadratic equation by ⁠ a {\displaystyle a} ⁠ to obtain a monic polynomial with the same roots. Namely, x 2 + b a x + c a = ( x − α ) ( x − β...

of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monic polynomial P in one variable...

necessarily have a monic polynomial, so finally multiply this by a constant to make it a monic polynomial. This will be the GCD of the two polynomials as it includes...

) {\displaystyle P(G,x)} is a monic polynomial of degree exactly n, with integer coefficients. The chromatic polynomial includes at least as much information...

all alternating polynomials, the Vandermonde polynomial is the lowest degree monic polynomial. Conversely, the Vandermonde polynomial is a factor of every...

gives a monic polynomial, whereas the alternative definition is monic only when n {\displaystyle n} is even. To compute the characteristic polynomial of the...

{k}{n}}}\right).} It may also be defined as the monic polynomial with integer coefficients that is the minimal polynomial over the field of the rational numbers...

is one of several distinct, although related, cubic polynomials defined from a monic polynomial of degree four: P ( x ) = x 4 + a 3 x 3 + a 2 x 2 + a...

In linear algebra, the Frobenius companion matrix of the monic polynomial p ( x ) = c 0 + c 1 x + ⋯ + c n − 1 x n − 1 + x n {\displaystyle p(x)=c_{0}+c_{1}x+\cdots...

concept of PI-algebra. If the degree of the polynomial P is defined in the usual way, the polynomial P is called monic if at least one of its terms of highest...

generic polynomial has a different, although related, meaning: a generic polynomial for a finite group G and a field F is a monic polynomial P with coefficients...

minimal polynomial of x. The minimal polynomial of an algebraic element x of L is irreducible, and is the unique monic irreducible polynomial of which...

polynomial of even degree 2d, then there is a polynomial q of degree d such that p(x) = xdq(x + ⁠1/x⁠). If p(x) is a monic antipalindromic polynomial...

division of polynomials, with less writing and fewer calculations than long division. It is mostly taught for division by linear monic polynomials (known as...

Chebyshev polynomials can also be characterized by the following theorem: If F n ( x ) {\displaystyle F_{n}(x)} is a family of monic polynomials with coefficients...

is said to be integral over a subring A of B if b is a root of some monic polynomial over A. If A, B are fields, then the notions of "integral over" and...

{Q}{c}}} is a monic polynomial, whose coefficients belong to any integral domain containing c and the coefficients of P. This polynomial transformation...

P(s)f(x)^{s+1}=b(s)f(x)^{s}.} The Bernstein–Sato polynomial is the monic polynomial of smallest degree amongst such polynomials b ( s ) {\displaystyle b(s)} . Its existence...

number is called a quadratic integer if it is a root of some monic polynomial (a polynomial whose leading coefficient is 1) of degree two whose coefficients...

establishes a link between algebra and geometry by showing that a monic polynomial (an algebraic object) in one variable with complex number coefficients...

determinant of ( λ I n − A ) {\displaystyle (\lambda I_{n}-A)} is a degree-n monic polynomial in λ, so it can be written as p A ( λ ) = λ n + c n − 1 λ n − 1 + ⋯...

Since L n ( α ) ( x ) {\displaystyle L_{n}^{(\alpha )}(x)} is a monic polynomial of degree n {\displaystyle n} in α {\displaystyle \alpha } , there...