mathematics, particularly p-adic analysis, the p-adic exponential function is a p-adic analogue of the usual exponential function on the complex numbers...
6 KB (772 words) - 02:21, 5 June 2025
Mittag-Leffler function, a generalization of the exponential function p-adic exponential function Padé table for exponential function – Padé approximation...
37 KB (5,070 words) - 18:51, 16 June 2025
In mathematics, p-adic analysis is a branch of number theory that studies functions of p-adic numbers. Along with the more classical fields of real and...
8 KB (1,043 words) - 18:51, 6 March 2025
Marshall–Olkin exponential distribution Matrix exponential Moore's law Nachbin's theorem Piano key frequencies p-adic exponential function Power law Proof...
6 KB (281 words) - 08:56, 22 January 2024
Valuation (algebra) (redirect from P-adic valuation of a Dedekind domain)
R), then the π-adic valuation and the π'-adic valuation are equal. Thus, the π-adic valuation can be called the P-adic valuation, where P = (π). The previous...
18 KB (2,370 words) - 06:59, 16 June 2025
Legendre's formula that the p-adic exponential function has radius of convergence p − 1 / ( p − 1 ) {\displaystyle p^{-1/(p-1)}} . Legendre, A. M. (1830)...
5 KB (1,036 words) - 16:24, 21 February 2025
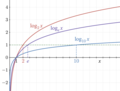
Logarithm (redirect from Logarithmic function)
(multi-valued) inverse function of the matrix exponential. Another example is the p-adic logarithm, the inverse function of the p-adic exponential. Both are defined...
98 KB (11,674 words) - 05:46, 10 June 2025
trigintaduonions etc.) p-adic function: a function whose domain is p-adic. Linear function; also affine function. Convex function: line segment between...
13 KB (1,407 words) - 00:18, 19 May 2025
e2πi = 1, in Cp, the field of p-adic complex numbers. p-adic exponential function Murty, M. Ram (2002). Introduction to P-Adic Analytic Number Theory. American...
2 KB (213 words) - 06:36, 27 May 2025
Collatz conjecture (section 2-adic extension)
2\right)2^{k}.} The function Q is a 2-adic isometry. Consequently, every infinite parity sequence occurs for exactly one 2-adic integer, so that almost...
57 KB (7,098 words) - 17:31, 28 May 2025
the degree as a rational function and for total degree of the associated L-function for a toric exponential sum, using the p-adic method developed by Bombieri...
16 KB (1,781 words) - 21:06, 5 June 2025
Lie group (redirect from P-adic Lie group)
\mathbb {Q} } , one can define a p-adic Lie group over the p-adic numbers, a topological group which is also an analytic p-adic manifold, such that the group...
65 KB (9,490 words) - 15:29, 22 April 2025
Exponentiation (redirect from Exponential functions)
integer Mathematics portal Double exponential function – Exponential function of an exponential function Exponential decay – Decrease in value at a rate...
105 KB (13,693 words) - 08:02, 16 June 2025
Pseudogamma function Hadamard's gamma function Inverse gamma function Lanczos approximation Multiple gamma function Multivariate gamma function p-adic gamma...
90 KB (13,517 words) - 14:18, 9 June 2025
Lindemann–Weierstrass theorem (redirect from Proof that p is transcendental)
\mathbb {Q} } , such that | αi |p < 1/p for all i; then the p-adic exponentials expp(α1), . . . , expp(αn) are p-adic numbers that are algebraically independent...
28 KB (4,778 words) - 00:16, 18 April 2025
Factorial (redirect from Factorial function)
the non-positive integers. In the p-adic numbers, it is not possible to continuously interpolate the factorial function directly, because the factorials...
70 KB (8,432 words) - 06:19, 30 April 2025
between the Artin–Hasse exponential and the regular exponential in the spirit of the ergodic perspective (linking the p-adic and regular norms over the...
7 KB (1,067 words) - 16:15, 6 November 2019
Number (section p-adic numbers)
set of the p-adic numbers contains the rational numbers, but is not contained in the complex numbers. The elements of an algebraic function field over...
66 KB (8,359 words) - 15:41, 10 June 2025
algebraic function with rational number coefficients. Through the theorem, it is readily demonstrable, for example, that the exponential function must be...
2 KB (285 words) - 16:49, 14 April 2025
applications for matrix-valued geometric series, function-valued geometric series, p {\displaystyle p} -adic number geometric series, and most generally geometric...
9 KB (1,594 words) - 09:00, 1 June 2025
Prime number (section p-adic numbers)
_{p}=p^{-\nu _{p}(q)}} . Multiplying an integer by its p {\displaystyle p} -adic absolute value cancels out the factors of p {\displaystyle p} ...
117 KB (14,179 words) - 21:25, 8 June 2025
operators on the symmetric space G/K. For semisimple p-adic Lie groups, the theory of zonal spherical functions and Hecke algebras was first developed by Satake...
49 KB (6,698 words) - 22:22, 23 May 2024
a subsystem of the 2-adic numbers as well as of the reals, and can represent the fractional parts of 2-adic numbers. Functions from natural numbers to...
35 KB (3,895 words) - 15:39, 26 March 2025
Weil conjectures (category Zeta and L-functions)
on the ℓ-adic cohomology group Hi. The rationality of the zeta function follows immediately. The functional equation for the zeta function follows from...
50 KB (7,942 words) - 17:39, 22 May 2025
other fields, such as fields of rational functions, algebraic function fields, algebraic number fields, and p-adic fields are commonly used and studied in...
87 KB (10,305 words) - 21:38, 10 June 2025
Complex number (section Complex exponential)
be regarded as its norm.] However for another inverse function of the complex exponential function (and not the above defined principal value), the branch...
91 KB (12,021 words) - 17:33, 29 May 2025
define the Theta functions over other fields where the exponential function might not be everywhere defined, such as fields of p-adic numbers. The Jacobi...
70 KB (14,667 words) - 23:32, 8 June 2025
exponent. Define the p-adic valuation νp(n) to be the exponent of the highest power of the prime p that divides n. That is, if p is one of the pi then...
53 KB (7,555 words) - 01:12, 6 April 2025
_{10}\left({\frac {d+1}{d}}\right)} . The tendency for real-world numbers to grow exponentially or logarithmically biases the distribution towards smaller leading digits...
32 KB (3,221 words) - 05:18, 5 June 2025
{-\ln(1-z)}{1-z}},} where ln(z) is the natural logarithm. An exponential generating function is ∑ n = 1 ∞ z n n ! H n = e z ∑ k = 1 ∞ ( − 1 ) k − 1 k z...
40 KB (5,560 words) - 19:11, 30 March 2025