The gamma function is an important special function in mathematics. Its particular values can be expressed in closed form for integer and half-integer...

Particular values of the gamma function for calculated values. It might be tempting to generalize the result that Γ ( 1 2 ) = π {\textstyle \Gamma \left({\frac...

particular values of the zeta function is difficult, often certain ratios can be found by inserting particular values of the gamma function into the functional...

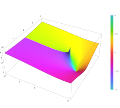
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems...

mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to...

{5}}+1)\end{array}}} Many values of the theta function and especially of the shown phi function can be represented in terms of the gamma function: φ ( exp ⁡ ( −...

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function: ψ ( z ) = d d z ln ⁡ Γ ( z ) = Γ ′ ( z ) Γ ( z )...

Gamma correction or gamma is a nonlinear operation used to encode and decode luminance or tristimulus values in video or still image systems. Gamma correction...

\mathrm {d} x} is the gamma function. The Riemann zeta function is defined for other complex values via analytic continuation of the function defined for σ...

distribution computations. The probability density and cumulative distribution functions of the gamma distribution vary based on the chosen parameterization...

extension of the factorial function to fractional arguments). Using explicit formulas for particular values of the gamma function at the integers and half integers...

Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of α {\displaystyle \alpha } . The most important...

formulas for particular values of the gamma function at the integers and half-integers gives formulas for the volume of a Euclidean ball in terms of factorials...

particular, according to the prime number theorem, it is a very good approximation to the prime-counting function, which is defined as the number of prime...

holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in...

mathematics, the multivariate gamma function Γp is a generalization of the gamma function. It is useful in multivariate statistics, appearing in the probability...

pieces of software use different close-by values (see below), or ignore the linear section, or use a plain gamma 2.2 function. The change in the images...

{1}{\pi }}\arctan \left({\frac {x-x_{0}}{\gamma }}\right)+{\frac {1}{2}}} and the quantile function (inverse cdf) of the Cauchy distribution is Q ( p ; x 0 ...

function at rational values. The Laurent series expansion for the Riemann zeta function*, where it is the first of the Stieltjes constants. Values of...

{\displaystyle C^{\gamma }-C^{\gamma -1}\pm \cdots +(-1)^{\gamma }C^{0}\geq b_{\gamma }(M)-b_{\gamma -1}(M)\pm \cdots +(-1)^{\gamma }b_{0}(M).} In particular, for any...

mathematics, the Chowla–Selberg formula is the evaluation of a certain product of values of the gamma function at rational values in terms of values of the Dedekind...

{\displaystyle n\geq 2} ; in particular Catalan's Constant β(2). (none of them are known to be irrational). Values of the Gamma Function Γ(1/n) for positive integers...

distribution. Just as extreme values of the normal distribution have low probability (and give small p-values), extreme values of the chi-squared distribution...

mathematics, the multiple gamma function Γ N {\displaystyle \Gamma _{N}} is a generalization of the Euler gamma function and the Barnes G-function. The double...

differential equations. In statistics, for non-negative real values of x, the error function has the following interpretation: for a real random variable Y...

mathematics, the reciprocal gamma function is the function f ( z ) = 1 Γ ( z ) , {\displaystyle f(z)={\frac {1}{\Gamma (z)}},} where Γ(z) denotes the gamma function...

where ν {\displaystyle \nu } is the number of degrees of freedom, and Γ {\displaystyle \Gamma } is the gamma function. This may also be written as f (...

continuous function that is close to their values to be zero everywhere. Instead, the p-adic gamma function provides a continuous interpolation of a modified...

a gamma-factor, involving the gamma function. This is now read as an 'extra' factor in the Euler product for the zeta-function, corresponding to the infinite...

In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If...