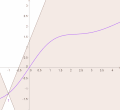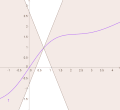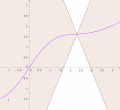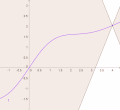
the Picard–Lindelöf theorem gives a set of conditions under which an initial value problem has a unique solution. It is also known as Picard's existence...

The Peano theorem can be compared with another existence result in the same context, the Picard–Lindelöf theorem. The Picard–Lindelöf theorem both assumes...

topology. Lindelöf spaces are named after him. He was the son of mathematician Lorenz Leonard Lindelöf and brother of the philologist Uno Lorenz Lindelöf [fi]...

Holmgren's uniqueness theorem for linear partial differential equations with real analytic coefficients. Picard–Lindelöf theorem, the uniqueness of solutions...

Picard's little theorem states that every nonconstant entire function takes every value in the complex plane, with perhaps one exception. Picard's great...

equations, Lipschitz continuity is the central condition of the Picard–Lindelöf theorem which guarantees the existence and uniqueness of the solution to...

value problem. Mathematics portal Picard–Lindelöf theorem Cauchy–Kowalevski theorem Coddington & Levinson (1955), Theorem 1.2 of Chapter 1 Coddington & Levinson...

provides a comparison theorem that can be used to prove uniqueness of a solution to the initial value problem; see the Picard–Lindelöf theorem. It is named for...

be applied to systems of equations. When the hypotheses of the Picard–Lindelöf theorem are satisfied, then local existence and uniqueness can be extended...

12 September 2010. Hörmander 1983, p. 56. Rudin 1991, Theorem 6.25. Stein & Weiss 1971, Theorem 1.18. Rudin 1991, §II.6.31. More generally, one only needs...

Lindelöf is a surname of Swedish origin which may refer to: Bernt Lindelöf, Swedish sprint canoeist who competed in the 1968 Summer Olympics Damon Lindelof...

equations Numerical methods for partial differential equations Picard–Lindelöf theorem on existence and uniqueness of solutions Recurrence relation, also...

p_{2})>qd(p_{1},p_{2}).} A standard application is the proof of the Picard–Lindelöf theorem about the existence and uniqueness of solutions to certain ordinary...

are assumed to be continuous and sufficiently smooth so that the Picard–Lindelöf theorem can be used to guarantee that solution x ( t ) {\displaystyle \mathbf...

condition given by the second condition (for instance, by the Picard–Lindelöf theorem). The parallel transport of X ∈ T γ ( s ) M {\displaystyle X\in...

Liénard's theorem (dynamical systems) Markus−Yamabe theorem (dynamical systems) Peano existence theorem (ordinary differential equations) Picard–Lindelöf theorem...

zero means that the function itself is specified. The Cauchy–Kowalevski theorem states that If all the functions F i {\displaystyle F_{i}} are analytic...

equal to zero, and whether it leads to a singular solution. The Picard–Lindelöf theorem, which gives sufficient conditions for unique solutions to exist...

t ) , y ′ ( t ) ) {\displaystyle y''(t)=f(t,y(t),y'(t))} . The Picard–Lindelöf theorem guarantees a unique solution on some interval containing t0 if...

the Cauchy–Kovalevskaya theorem (also written as the Cauchy–Kowalevski theorem) is the main local existence and uniqueness theorem for analytic partial differential...

differential equations, whose solvability is guaranteed by the Picard–Lindelöf theorem. If the vector field X {\displaystyle X} is nowhere zero then it...

Existence and uniqueness Picard–Lindelöf theorem Peano existence theorem Carathéodory's existence theorem Cauchy–Kowalevski theorem General topics Initial...

b,c\in X.} The Lipschitz condition occurs, for example, in the Picard–Lindelöf theorem concerning the solutions of ordinary differential equations. Another...

Existence and uniqueness Picard–Lindelöf theorem Peano existence theorem Carathéodory's existence theorem Cauchy–Kowalevski theorem General topics Initial...

Existence and uniqueness Picard–Lindelöf theorem Peano existence theorem Carathéodory's existence theorem Cauchy–Kowalevski theorem General topics Initial...

Existence and uniqueness Picard–Lindelöf theorem Peano existence theorem Carathéodory's existence theorem Cauchy–Kowalevski theorem General topics Initial...

Existence and uniqueness Picard–Lindelöf theorem Peano existence theorem Carathéodory's existence theorem Cauchy–Kowalevski theorem General topics Initial...

order at least two. This is the main result of Picard–Vessiot theory which was initiated by Émile Picard and Ernest Vessiot, and whose recent developments...

whenever the real part of a {\displaystyle a} is negative. The Picard–Lindelöf theorem, which shows that ordinary differential equations have solutions...

work on the latter allowed Émile Picard to show solutions of differential equations exist (the Picard–Lindelöf theorem). In 1892 he became a member of...