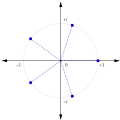
In field theory, a primitive element of a finite field GF(q) is a generator of the multiplicative group of the field. In other words, α ∈ GF(q) is called...

In finite field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite field GF(pm). This...

extension Primitive element (finite field), an element that generates the multiplicative group of a finite field Primitive element (lattice), an element in a...

completely classified. The primitive element theorem provides a characterization of the finite simple extensions. A field extension L/K is called a simple...

finite field or Galois field (so-named in honor of Évariste Galois) is a field that contains a finite number of elements. As with any field, a finite...

In field theory, the primitive element theorem states that every finite separable field extension is simple, i.e. generated by a single element. This theorem...

up primitive in Wiktionary, the free dictionary. Primitive may refer to: Primitive element (field theory) Primitive element (finite field) Primitive cell...

mathematics, finite field arithmetic is arithmetic in a finite field (a field containing a finite number of elements) contrary to arithmetic in a field with an...

characteristic 0, every finite extension is a simple extension. This is the primitive element theorem, which does not hold true for fields of non-zero characteristic...

the group set such that every element of the group can be expressed as a combination (under the group operation) of finitely many elements of the subset...

Finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical...

(h(a))} . A primitive normal basis of an extension of finite fields E / F is a normal basis for E / F that is generated by a primitive element of E, that...

roots belong to a finite field, and, conversely, every nonzero element of a finite field is a root of unity. Any algebraically closed field contains exactly...

mathematics, an idempotent element or simply idempotent of a ring is an element a such that a2 = a. That is, the element is idempotent under the ring's...

definition, those that are separable and normal. The primitive element theorem shows that finite separable extensions are necessarily simple, i.e., of...

In mathematics, a permutation group G acting on a non-empty finite set X is called primitive if G acts transitively on X and the only partitions the G-action...

Finite Field Diffie–Hellman in RFC 7919, of the protocol uses the multiplicative group of integers modulo p, where p is prime, and g is a primitive root...

compact element. This notion of compactness simultaneously generalizes the notions of finite sets in set theory, compact sets in topology, and finitely generated...

called primitive roots modulo n. For a prime number p, the group (Z/pZ)× is always cyclic, consisting of the non-zero elements of the finite field of order p...

the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could...

over F. Primitive element An element α of an extension field E over a field F is called a primitive element if E=F(α), the smallest extension field containing...

finite fields. The notions of irreducible polynomial and of algebraic field extension are strongly related, in the following way. Let x be an element...

representation theory that studies linear representations of finite groups over a field K of positive characteristic p, necessarily a prime number. As...

right-most element appearing on the left), when referred to the natural basis 1, g, g2, ..., gn−1. When the field K contains a primitive n-th root of...

number fields, a fundamental step is a factorization of a polynomial over a finite field. Polynomial rings over the integers or over a field are unique...

definition, is always abelian. If a field K contains a primitive n-th root of unity and the n-th root of an element of K is adjoined, the resulting Kummer...

finite ring is a ring that has a finite number of elements. Every finite field is an example of a finite ring, and the additive part of every finite ring...

integer is an integral element of a finite extension K / Q {\displaystyle K/\mathbb {Q} } . Note that if P(x) is a primitive polynomial that has integer...

Such an element a {\displaystyle a} is called a generator or a primitive element of the group. In additive notation, the requirement for an element to be...

field theory, Steinitz's theorem states that a finite extension of fields L / K {\displaystyle L/K} is simple if and only if there are only finitely many...