{\displaystyle f.} The most commonly encountered symmetric functions are polynomial functions, which are given by the symmetric polynomials. A related notion is alternating...

important role in the representation theory of the symmetric group. The ring of symmetric functions can be given a coproduct and a bilinear form making...

a symmetric function if p ( − x ) = p ( x ) {\displaystyle p(-x)=p(x)} for all x ∈ X . {\displaystyle x\in X.} Every subadditive symmetric function is...

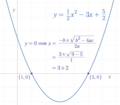
is self-symmetric with respect to the origin. If the domain of a real function is self-symmetric with respect to the origin, then the function can be uniquely...

the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial can be...

a symmetric polynomial if for any permutation σ of the subscripts 1, 2, ..., n one has P(Xσ(1), Xσ(2), ..., Xσ(n)) = P(X1, X2, ..., Xn). Symmetric polynomials...

The elements of the symmetric group on a set X are the permutations of X. The group operation in a symmetric group is function composition, denoted by...

The chromatic symmetric function is a symmetric function invariant of graphs studied in algebraic graph theory, a branch of mathematics. It is the weight...

from its transformed image is called mirror symmetric. In formal terms, a mathematical object is symmetric with respect to a given operation such as reflection...

the Stanley symmetric functions are a family of symmetric functions introduced by Richard Stanley (1984) in his study of the symmetric group of permutations...

In mathematics, a symmetric Boolean function is a Boolean function whose value does not depend on the order of its input bits, i.e., it depends only on...

algebra, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomials. Every symmetric polynomial can be expressed as a...

sometimes called the symmetric difference quotient. A function is said to be symmetrically differentiable at a point x if its symmetric derivative exists...

Boolean ring, with symmetric difference as the addition of the ring and intersection as the multiplication of the ring. The symmetric difference is equivalent...

drawbacks of symmetric-key encryption, in comparison to public-key encryption (also known as asymmetric-key encryption). However, symmetric-key encryption...

mathematics, the noncommutative symmetric functions form a Hopf algebra NSymm analogous to the Hopf algebra of symmetric functions. The Hopf algebra NSymm was...

often used in the analysis of spherically symmetric or axially symmetric functions. The Abel transform of a function f(r) is given by F ( y ) = 2 ∫ y ∞ f (...

potential applications, from symmetric function theory to quantum chemistry studies of atoms, molecules and solids. The symmetric group Sn has order n!. Its...

ω involution on the ring of symmetric functions, one obtains the dual Pieri rule for multiplying an elementary symmetric polynomial with a Schur polynomial:...

the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with...

⁠ are symmetric polynomials in ⁠ α {\displaystyle \alpha } ⁠ and ⁠ β {\displaystyle \beta } ⁠. Specifically, they are the elementary symmetric polynomials...

from kernel methods. In general, a kernel is a positive-semidefinite symmetric function of two inputs which represents some notion of similarity between the...

Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete...

give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of...

symmetrization is a process that converts any function in n {\displaystyle n} variables to a symmetric function in n {\displaystyle n} variables. Similarly...

{X}}} be a nonempty set, sometimes referred to as the index set. A symmetric function K : X × X → R {\displaystyle K:{\mathcal {X}}\times {\mathcal {X}}\to...

continuity implies symmetric continuity, but the converse is not true. For example, the function x − 2 {\displaystyle x^{-2}} is symmetrically continuous at...

countable number of variables. This ring generalizes the ring of symmetric functions. This ring can be realized as a specific limit of the rings of quasisymmetric...

exponential function, translates addition into multiplication. This exponential operator appears naturally in the theory of symmetric functions, as a concise...

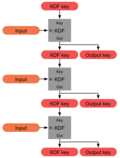
key exchange into a symmetric key for use with AES. Keyed cryptographic hash functions are popular examples of pseudorandom functions used for key derivation...