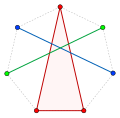
In discrete geometry, Tverberg's theorem, first stated by Helge Tverberg in 1966, is the result that sufficiently many points in Euclidean space can be...

Russo–Dye theorem describes the convex hulls of unitary elements in a C*-algebra. In discrete geometry, both Radon's theorem and Tverberg's theorem concern...

to zero somewhere, which is the point of Tverberg's Lemma 4. The first formal proof of the Jordan curve theorem was created by Hales (2007a) in the HOL...

Helly's theorem Kirchberger's theorem N-dimensional polyhedron Radon's theorem, and its generalization Tverberg's theorem Krein–Milman theorem Choquet...

Tverberg may refer to: Helge Tverberg (1935–2020), Norwegian mathematician Ryan Tverberg (born 2002), Canadian ice hockey player Tverberg's theorem, mathematics...

point. Tverberg's theorem. A generalization for partition into r sets was given by Helge Tverberg (1966) and is now known as Tverberg's theorem. It states...

Radon's theorem, and its generalization, Tverberg's theorem Cantor's intersection theorem - another theorem on intersection of sets Helly Family Danzer...

hyperplane theorem (convex geometry) Sylvester–Gallai theorem (plane geometry) Szemerédi–Trotter theorem (combinatorics) Tverberg's theorem (discrete geometry)...

real numbers for infinitely many values of n. In connection with Tverberg's theorem, Bárány & Larman (1992) conjectured that, for every set of r (d + 1)...

{\displaystyle \delta =\delta (k,d)<1} . This result follows from the colored Tverberg theorem. It is far from the conjectured bound of O ( n d ) {\displaystyle O(n^{d})}...

theorem. It inaugurated a new branch of combinatorial geometry, with many variations and applications. An account by Günter M. Ziegler of Tverberg's work...

spaces, and topological and multicolored variants of Radon's theorem and Tverberg's theorem on partitions into subsets with intersecting convex hulls. The...

also possible. The proof of the Graham–Pollak theorem described by Aigner & Ziegler (2018) (following Tverberg 1982) defines a real variable x i {\displaystyle...

aspect; e.g., the pseudoachromatic number from graph theory and the Tverberg theorem from combinatorial convexity are simply two faces of the same aspect...

formula Ferrers graph Glaisher's theorem Landau's function Partition function (number theory) Pentagonal number theorem Plane partition Quotition and partition...

Shlosman and A.Szucs (1981). "On a topological generalization of a theorem of Tverberg". Journal of the London Mathematical Society. 2 (23): 158–164. CiteSeerX 10...

continuously shrunk to a single point. This can be proved using the Borsuk–Ulam theorem. Proving that conn π ( S d ) ≥ d − 1 {\displaystyle {\text{conn}}_{\pi...

Another argument for the impossibility of circular realizations, by Helge Tverberg, uses inversive geometry to transform any three circles so that one of...

1993, Andrew Wiles used the Selmer group in his proof of Fermat's last theorem. Selmer received his dr.philos in 1952 from the University of Oslo and...

induction on d, it is possible to generalize the above theorem to d dimensions and get the following theorem: Given N axis-parallel d-boxes whose interiors are...