a cardinal function (or cardinal invariant) is a function that returns cardinal numbers. The most frequently used cardinal function is the function that...

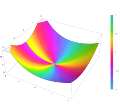
entire function. The function has also been called the cardinal sine or sine cardinal function. The term sinc is a contraction of the function's full Latin...

related to Cardinality. Wikidata has the properties: group cardinality (P1164) (see uses) cardinality of this set (P2820) (see uses) Cardinal function Inaccessible...

an early conception of cardinality. Bernoulli's imaginary logarithmic utility function and Gabriel Cramer's U = W1/2 function were conceived at the time...

rank among the infinite cardinals. Cardinality is defined in terms of bijective functions. Two sets have the same cardinality if, and only if, there is...

number Gimel function Regular cardinal Infinity Transfinite number Ordinal number Given the axiom of choice, every infinite set has a cardinality that is an...

potentials and Massieu functions. The entropy as a function only of extensive state variables is the one and only cardinal function of state for the generation...

In axiomatic set theory, the gimel function is the following function mapping cardinal numbers to cardinal numbers: ℷ : κ ↦ κ c f ( κ ) {\displaystyle...

surjective function (also known as surjection, or onto function /ˈɒn.tuː/) is a function f such that, for every element y of the function's codomain, there...

Parameter p-adic number Cardinality Valency (linguistics) n-ary code n-ary group Function prototype – Declaration of a function's name and type signature...

if, for every function f: [κ]<ω → {0, 1} there is a set A of cardinality κ that is homogeneous for f. That is, for every n, the function f is constant...

In mathematics, an injective function (also known as injection, or one-to-one function ) is a function f that maps distinct elements of its domain to...

In mathematics, the domain of a function is the set of inputs accepted by the function. It is sometimes denoted by dom ⁡ ( f ) {\displaystyle \operatorname...

two sets are said to have the same cardinal number if there exists a bijection between them. A bijective function from a set to itself is also called...

Computable functions are the basic objects of study in computability theory. Informally, a function is computable if there is an algorithm that computes...

A cardinal is a senior member of the clergy of the Catholic Church. As titular members of the clergy of the Diocese of Rome, they serve as advisors to...

voting) functions only use ordinal information, i.e. whether one choice is better than another. Cardinal (or rated voting) functions also use cardinal information...

of a function is a value provided to obtain the function's result. It is also called an independent variable. For example, the binary function f ( x...

cardinality, a bijection being provided by the function ⁠ x ↦ tan ⁡ ( π x / 2 ) {\displaystyle x\mapsto \tan(\pi x/2)} ⁠. Having the same cardinality...

field of set theory, a large cardinal property is a certain kind of property of transfinite cardinal numbers. Cardinals with such properties are, as the...

a function may refer either to the codomain of the function, or the image of the function. In some cases the codomain and the image of a function are...

counter-domain, or set of destination of a function is a set into which all of the output of the function is constrained to fall. It is the set Y in the...

cardinal is a cardinal number that is equal to its own cofinality. More explicitly, this means that κ {\displaystyle \kappa } is a regular cardinal if...

transitions between two bundles of goods. A cardinal utility function can be transformed to another utility function by a positive linear transformation (multiplying...

countable if the set of function and relation symbols in it is countable, and in general the cardinality of a signature is the cardinality of the set of all...

Moore space question was eventually proved to be independent of ZFC. Cardinal functions are widely used in topology as a tool for describing various topological...

That is, X is nonempty and there is no surjective function from the natural numbers to X. The cardinality of X is neither finite nor equal to ℵ 0 {\displaystyle...

induction to well-ordered sets, for example to sets of ordinal numbers or cardinal numbers. Its correctness is a theorem of ZFC. Let P ( α ) {\displaystyle...

cardinal, also called a partition cardinal is a certain kind of large cardinal number introduced by Paul Erdős and András Hajnal (1958). A cardinal κ...

1016/0024-3795(95)00705-9. ISSN 0024-3795. Whittaker, J. M. (May 1927). "On the Cardinal Function of Interpolation Theory". Proceedings of the Edinburgh Mathematical...