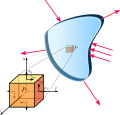
the Cauchy stress tensor (symbol σ {\displaystyle {\boldsymbol {\sigma }}} , named after Augustin-Louis Cauchy), also called true stress tensor or simply...

orientation of S. Thus the stress state of the material must be described by a tensor, called the (Cauchy) stress tensor; which is a linear function...

constitutive models (for example, the Cauchy Stress tensor is variant to a pure rotation, while the deformation strain tensor is invariant; thus creating problems...

measure of stress is the Cauchy stress tensor, often called simply the stress tensor or "true stress". However, several alternative measures of stress can be...

of Cauchy stress tensor, σ I , σ I I , σ I I I {\displaystyle {{\sigma }_{I}},{{\sigma }_{II}},{{\sigma }_{III}}}  denote principal values of Cauchy stress...

relativity (stress–energy tensor, curvature tensor, ...). In applications, it is common to study situations in which a different tensor can occur at...

the material rate of the Cauchy stress tensor, and L {\displaystyle {\boldsymbol {L}}} is the spatial velocity gradient tensor. If only these two original...

_{v}^{2}=3J_{2}=3k^{2}} Substituting J 2 {\displaystyle J_{2}} with the Cauchy stress tensor components, we get σ v 2 = 1 2 [ ( σ 11 − σ 22 ) 2 + ( σ 22 − σ 33...

of the stress increment tensor on the strain increment tensor be correct (work conjugacy requirement). The relation between the Cauchy stress and the...

Gravitational stress-energy tensor The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical...

of the Cauchy stress tensor and infinitesimal strain tensor, and C i j k l {\displaystyle C^{ijkl}} are the components of the elasticity tensor. Summation...

two-dimensional graphical representation of the transformation law for the Cauchy stress tensor. Mohr's circle is often used in calculations relating to mechanical...

Stress tensor may refer to: Cauchy stress tensor, in classical physics Stress deviator tensor, in classical physics Piola–Kirchhoff stress tensor, in...

of tensor theory. For expositions of tensor theory from different points of view, see: Tensor Tensor (intrinsic definition) Application of tensor theory...

}}\nabla \cdot {\boldsymbol {\sigma }}+\mathbf {f} .} By setting the Cauchy stress tensor σ {\textstyle {\boldsymbol {\sigma }}} to be the sum of a viscosity...

the Cauchy stress tensor. This part is given by the normal stresses that occur in almost all situations. The anisotropic part of the stress tensor gives...

gradient to the first or second Piola-Kirchhoff stress tensor. For an isotropic material the Cauchy stress tensor σ {\displaystyle {\boldsymbol {\sigma }}}...

Use of Cartesian tensors occurs in physics and engineering, such as with the Cauchy stress tensor and the moment of inertia tensor in rigid body dynamics...

The viscous stress tensor is a tensor used in continuum mechanics to model the part of the stress at a point within some material that can be attributed...

principal stresses (the eigenvalues of the Cauchy stress tensor) is zero. That is, there is Cartesian coordinate system in which the stress tensor has the...

{\boldsymbol {\sigma }}} is the Cauchy stress tensor, ε {\displaystyle {\boldsymbol {\varepsilon }}} is the infinitesimal strain tensor, u {\displaystyle \mathbf...

{C}}}}~.} This stress tensor can subsequently be converted into any of the other conventional stress tensors, such as the Cauchy stress tensor which is given...

spacetime Tensor – Algebraic object with geometric applications Tensor density – Generalization of tensor fields Tensor field – Assignment of a tensor continuously...

In multilinear algebra, a tensor contraction is an operation on a tensor that arises from the canonical pairing of a vector space and its dual. In components...

principle, that means determining, implicitly or explicitly, the Cauchy stress tensor at every point. The external forces may be body forces (such as gravity...

various areas, including: Classical treatment of tensors Dyadic tensor Glossary of tensor theory Metric tensor Bra–ket notation Multilinear subspace learning...

electromagnetism, the electromagnetic tensor or electromagnetic field tensor (sometimes called the field strength tensor, Faraday tensor or Maxwell bivector) is a...

In tensor analysis, a mixed tensor is a tensor which is neither strictly covariant nor strictly contravariant; at least one of the indices of a mixed...

deformation tensor (called the Cauchy strain tensor in that document), i. e., C − 1 {\displaystyle \mathbf {C} ^{-1}} , be called the Finger strain tensor. However...

inertia tensor of a body calculated at its center of mass, and R {\displaystyle \mathbf {R} } be the displacement vector of the body. The inertia tensor of...