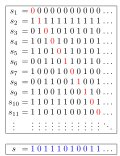
In constructive mathematics, Church's thesis C T {\displaystyle {\mathrm {CT} }} is the principle stating that all total functions are computable functions...

the Church–Turing thesis (also known as computability thesis, the Turing–Church thesis, the Church–Turing conjecture, Church's thesis, Church's conjecture...

Constructive analysis Church's thesis (constructive mathematics) Limited principle of omniscience Margenstern, Maurice (1995). "L'école constructive de...

Axiom schema of predicative separation Constructive mathematics Constructive analysis Constructive Church's thesis rule and principle Computable set Diaconescu's...

1928 using intuitionistic principles, and can also be proven using Church's thesis. The analogous property in classical analysis is the fact that every...

In mathematics, constructive analysis is mathematical analysis done according to some principles of constructive mathematics. The name of the subject...

Hilbert and Bernays, the constructive recursive mathematics of mathematicians Shanin and Markov, and Bishop's program of constructive analysis. Constructivism...

computable Church's thesis (constructive mathematics), an axiom in constructive mathematics which states that all total functions are computable Church (disambiguation)...

Robin, 1978, Church's Thesis and the Principles for Mechanisms, in (Barwise et al. 1980:123-148) George, Alexander (+ed.), 1994, Mathematics and Mind, 216...

In mathematics, an expression is a written arrangement of symbols following the context-dependent, syntactic conventions of mathematical notation. Symbols...

Principles of Mathematical Logic. AMS Chelsea Publishing, Providence, Rhode Island, USA, 1950 Church's paper was presented to the American Mathematical Society...

In mathematics, and particularly in set theory, category theory, type theory, and the foundations of mathematics, a universe is a collection that contains...

Mathematical induction is a method for proving that a statement P ( n ) {\displaystyle P(n)} is true for every natural number n {\displaystyle n} , that...

Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining...

many adherents, and it was not until Bishop's work in 1967 that constructive mathematics was placed on a sounder footing. One may consider that Hilbert's...

particularly the proof theory of constructive mathematics based on the Curry–Howard correspondence, one often identifies a mathematical proposition with its set...

published by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of mathematics. The theorems are widely, but not universally,...

corresponding parts, with part D being about "Proof Theory and Constructive Mathematics". Prawitz (1965, p. 98). Girard, Taylor & Lafont 2003. Chaudhuri...

to solve the problem by changing of logical framework, such as constructive mathematics and intuitionistic logic. Roughly speaking, the first one consists...

them the infinite can never be completed: In classical mathematics there occur non-constructive or indirect existence proofs, which intuitionists do not...

halting problem. In response, Tegmark notes: sec. V.E  that a constructive mathematics formalized measure of free parameter variations of physical dimensions...

constructive methods and algorithms to find numerical approximations (as opposed to symbolic manipulations) of solutions to problems in mathematical analysis...

"Turing's Thesis", asserting the identity of computability in general with computability by Turing machines, as an equivalent form of Church's Thesis. 1954...

In mathematics, a structure on a set (or on some sets) refers to providing or endowing it (or them) with certain additional features (e.g. an operation...

{\displaystyle S} and a subset of S {\displaystyle S} . Also in constructive mathematics, there is no surjection from the full domain N {\displaystyle {\mathbb...

In mathematics, Church encoding is a means of representing data and operators in the lambda calculus. The Church numerals are a representation of the...

(1903–1979), was also a notable mathematician, making contributions to constructive mathematics and recursive function theory. Andrey Markov was born on 14 June...

model are computable for the above four models of computation. The Church–Turing thesis is the unprovable assertion that every notion of computability that...

choice is avoided in some varieties of constructive mathematics, although there are varieties of constructive mathematics in which the axiom of choice is embraced...

set theory model theory recursion theory, and proof theory and constructive mathematics (considered as parts of a single area). Additionally, sometimes...