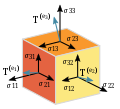
elasticity tensor is a fourth-rank tensor describing the stress-strain relation in a linear elastic material. Other names are elastic modulus tensor and...

deformation tensors. In 1839, George Green introduced a deformation tensor known as the right Cauchy–Green deformation tensor or Green's deformation tensor (the...

mechanics (stress, elasticity, quantum mechanics, fluid mechanics, moment of inertia, ...), electrodynamics (electromagnetic tensor, Maxwell tensor, permittivity...

is used is the infinitesimal strain tensor; the resulting (predicted) material behavior is termed linear elasticity, which (for isotropic media) is called...

the first and second Piola–Kirchhoff stress tensors, the Biot stress tensor, and the Kirchhoff stress tensor. Bending Compressive strength Critical plane...

is a fourth-order tensor (that is, a linear map between second-order tensors) usually called the stiffness tensor or elasticity tensor. One may also write...

{1}}}} be the second order identity tensor. Then the derivative of this tensor with respect to a second order tensor A {\displaystyle {\boldsymbol {A}}}...

moments) and the produced deflection are the coupling stiffnesses. The elasticity tensor is a generalization that describes all possible stretch and shear...

Proportional limit Stiffness Tensile strength Transverse isotropy Elasticity tensor Askeland, Donald R.; Phulé, Pradeep P. (2006). The science and engineering...

tensor (symbol σ {\displaystyle {\boldsymbol {\sigma }}} , named after Augustin-Louis Cauchy), also called true stress tensor or simply stress tensor...

of Elasticity, Dover, ISBN 0-486-67865-2 P.C. Chou, N. J. Pagano, Elasticity: Tensor, Dyadic, and Engineering Approaches, Dover, ISBN 0-486-66958-0 R.W...

tensors used in finite strain theory, e.g. the Lagrangian finite strain tensor E {\displaystyle \mathbf {E} } , and the Eulerian finite strain tensor...

notation and manipulation for tensors and tensor fields on a differentiable manifold, with or without a metric tensor or connection. It is also the modern...

characteristic directions; such as the principal directions of its elasticity tensor. Uni-directional ply's for example always have their first axis aligned...

ISO 80000-4 (Mechanics), as a "tensor quantity representing the deformation of matter caused by stress. Strain tensor is symmetric and has three linear...

Curvilinear Coordinates Wikiversity:Introduction to Elasticity/Tensors#The divergence of a tensor field – Wikiversity, Introduction to Elasticity/Tensors....

ceases to be true for tensors of rank 6 and higher), so the number of independent constants in the (fourth-rank) elasticity tensor are reduced to 5 (from...

_{0}\left({\partial ^{2} \over \partial \Omega ^{2}}u\right)_{\Omega =\Omega _{0}}} Elasticity tensor Volumetric strain "Bulk Elastic Properties". hyperphysics. Georgia...

rate tensor, C {\textstyle \mathbf {C} } is the fourth-order tensor representing the constant of proportionality, called the viscosity or elasticity tensor...

stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Young's modulus is defined as the ratio...

rate tensor, C {\textstyle \mathbf {C} } is the fourth-order tensor representing the constant of proportionality, called the viscosity or elasticity tensor...

infinitesimal strain and L i j k l {\displaystyle L_{ijkl}} is the elasticity tensor, a fourth-rank tensor with 81 components (usually 21 independent components)...

{\sigma }}} is the Cauchy stress tensor, ε {\displaystyle {\boldsymbol {\varepsilon }}} is the infinitesimal strain tensor, u {\displaystyle \mathbf {u}...

learning, the term tensor informally refers to two different concepts (i) a way of organizing data and (ii) a multilinear (tensor) transformation. Data...

single component of a tensor. Clockwork Elasto-capillarity Rubber elasticity Landau, L.D.; Lifshitz, E. M. (1986). Theory of Elasticity (3rd ed.). Oxford...

differential geometry, the torsion tensor is a tensor that is associated to any affine connection. The torsion tensor is a bilinear map of two input vectors...

of tensor theory. For expositions of tensor theory from different points of view, see: Tensor Tensor (intrinsic definition) Application of tensor theory...

is the stress tensor, ε the strain tensor, I the identity matrix and tr the trace function. Hooke's law may be written in terms of tensor components using...

a Cartesian tensor uses an orthonormal basis to represent a tensor in a Euclidean space in the form of components. Converting a tensor's components from...

= lim t → ∞ G ( t ) {\displaystyle G=\lim _{t\to \infty }G(t)} . Elasticity tensor Dynamic modulus Impulse excitation technique Shear strength Seismic...