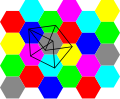
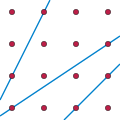
geometry, the Erdős distinct distances problem states that every set of points in the plane has a nearly-linear number of distinct distances. It was posed...

according to the 2015 solution of the Erdős distinct distances problem by Larry Guth and Nets Katz, the distance set of any finite collection of points...

The Erdős–Menger conjecture on disjoint paths in infinite graphs, proved by Ron Aharoni and Eli Berger in 2009. The Erdős distinct distances problem. The...

The Erdős Distance Problem is a monograph on the Erdős distinct distances problem in discrete geometry: how can one place n {\displaystyle n} points into...

Willmore conjecture (Fernando Codá Marques and André Neves, 2012) Erdős distinct distances problem (Larry Guth, Nets Hawk Katz, 2011) Heterogeneous tiling conjecture...

{Z} _{4}^{n}} by Croot, Lev and Pach The Erdős distinct distances problem by Guth and Katz The Joints Problem in 3D by Guth and Katz. Their argument was...

discrepancy problem Erdős distinct distances problem Burr–Erdős conjecture Cameron–Erdős conjecture Erdős–Faber–Lovász conjecture Erdős–Graham conjecture...

analogue of the Erdős distinct distances problem, which states that large finite sets of points must have large numbers of distinct distances. Based on this...

Her dissertation, Distribution of Distances in Finite Point Sets, is connected to the Erdős distinct distances problem and was supervised by Vera Sós. Vesztergombi's...

Salem–Spencer set Secretary problem Tournament (graph theory) Erdős distinct distances problem Leo Moser at the Mathematics Genealogy Project W. Moser, G...

published the results of their collaborative effort to solve the Erdős distinct distances problem, in which they found a "near-optimal" result, proving that...

[ME] and for the Erdős distinct distances problem, showing that every set of points in the plane has many different pairwise distances.[DD] In 2006, Solymosi...

away a person is from prolific mathematician Paul Erdős and actor Kevin Bacon, respectively—are distances in the graphs whose edges represent mathematical...

manifolds and, along with Nets Katz, found a solution to the Erdős distinct distances problem. His interests include the Kakeya conjecture and the systolic...

in turn, enabled Katz and Guth to solve the Erdős distinct distances problem, a 1946 problem of Erdős. Work continues on improvements in Purdy's conjecture...

which eventually led Guth and Katz to the solution of the Erdős distinct distances problem. (See below.) After graduating from the mathematics program...

Petersen graphs are non-strict unit distance graphs. An unsolved problem of Paul Erdős asks how many edges a unit distance graph on n {\displaystyle n} vertices...

chromatic number of the plane". By the de Bruijn–Erdős theorem, a result of de Bruijn & Erdős (1951), the problem is equivalent (under the assumption of the...

other model contemporaneously with and independently of Erdős and Rényi. In the model of Erdős and Rényi, all graphs on a fixed vertex set with a fixed...

getting wet. The problem was first posed in 1962 by Basil Gordon (although it has sometimes been erroneously attributed to Paul Erdős) and it remains unsolved...

reciprocals of positive integers. According to the proof of the Erdős–Graham problem, if the set of integers greater than one is partitioned into finitely...

Ngô Bảo Châu. 2010 – Larry Guth and Nets Hawk Katz solve the Erdős distinct distances problem. 2013 – Yitang Zhang proves the first finite bound on gaps...

the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao...

assumption of the axiom of choice. This is the de Bruijn–Erdős theorem of de Bruijn & Erdős (1951). If a graph admits a full n-coloring for every n ≥...

Erdős–Mordell inequality; a stronger variant of it is Barrow's inequality, which replaces the perpendicular distances to the sides with the distances...

introduction of probabilistic methods in graph theory, especially in the study of Erdős and Rényi of the asymptotic probability of graph connectivity, gave rise...

Research problems in discrete geometry, Berlin: Springer, ISBN 0-387-23815-8 de Bruijn, N. G.; Erdős, P. (1948), "A combinatioral [sic] problem" (PDF),...

"immersion", but many graph theorists, including Erdős, Harary and Tutte, use the term "embedding". Erdős, P.; Harary, F.; Tutte, W. T. (1965). "On the dimension...

elliptic curve. A negative solution to the Erdős–Ulam problem on dense sets of Euclidean points with rational distances. An effective version of Siegel's theorem...

important in sociology and anthropology Erdős number – Closeness of someone's association with mathematician Paul Erdős Erdős–Bacon number – Closeness of someone's...