In graph theory, graph coloring is a methodic assignment of labels traditionally called "colors" to elements of a graph. The assignment is subject to certain...

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color...

registers representing available colors) would be a coloring for the original graph. As Graph Coloring is an NP-Hard problem and Register Allocation is in...

graph theory, total coloring is a type of graph coloring on the vertices and edges of a graph. When used without any qualification, a total coloring is...

as is required in the graph coloring problem. In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a triangle: after...

In graph theory, a complete coloring is a (proper) vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently...

of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed...

the vertex coloring game on a graph G with k colors. Does she have one for k+1 colors? More unsolved problems in mathematics The graph coloring game is a...

arboricity of a graph. Degeneracy is also known as the k-core number, width, and linkage, and is essentially the same as the coloring number or Szekeres–Wilf...

vertex sets of two graphs that maps adjacent vertices to adjacent vertices. Homomorphisms generalize various notions of graph colorings and allow the expression...

Fractional coloring is a topic in a branch of graph theory known as fractional graph theory. It is a generalization of ordinary graph coloring. In a traditional...

The coloring of maps can also be stated in terms of graph theory, by considering it in terms of constructing a graph coloring of the planar graph of adjacencies...

is a type of graph coloring that combines list coloring and edge coloring. An instance of a list edge-coloring problem consists of a graph together with...

colorings and cliques in those families. For instance, in all perfect graphs, the graph coloring problem, maximum clique problem, and maximum independent set problem...

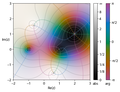
In complex analysis, domain coloring or a color wheel graph is a technique for visualizing complex functions by assigning a color to each point of the...

In graph theory, an acyclic coloring is a (proper) vertex coloring in which every 2-chromatic subgraph is acyclic. The acyclic chromatic number A(G) of...

In graph theory, a distinguishing coloring or distinguishing labeling of a graph is an assignment of colors or labels to the vertices of the graph that...

In graph theory, a branch of mathematics, list coloring is a type of graph coloring where each vertex can be restricted to a list of allowed colors. It...

of a graph is the maximum number of colors in a complete coloring. acyclic 1.  A graph is acyclic if it has no cycles. An undirected acyclic graph is the...

In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that No...

the resolution of extremal graph theory problems. A proper (vertex) coloring of a graph G {\displaystyle G} is a coloring of the vertices of G {\displaystyle...

In graph theory, a weak coloring is a special case of a graph labeling. A weak k-coloring of a graph G = (V, E) assigns a color c(v) ∈ {1, 2, ..., k}...

Goldberg–Seymour conjecture Graph coloring game Graph two-coloring Harmonious coloring Incidence coloring List coloring List edge-coloring Perfect graph Ramsey's theorem...

In graph theory, an exact coloring is a (proper) vertex coloring in which every pair of colors appears on exactly one pair of adjacent vertices. That...

In graph theory, a uniquely colorable graph is a k-chromatic graph that has only one possible (proper) k-coloring up to permutation of the colors. Equivalently...

Hamiltonian coloring, named after William Rowan Hamilton, is a type of graph coloring. Hamiltonian coloring uses a concept called detour distance between...

positive integer 2. A coloring may or may not exist for a mixed graph. In order for a mixed graph to have a k-coloring, the graph cannot contain any directed...

number of colors that can be used by a greedy coloring strategy that considers the vertices of the graph in sequence and assigns each vertex its first...

problems and theorems in graph theory have to do with various ways of coloring graphs. Typically, one is interested in coloring a graph so that no two adjacent...

complete bipartite graph Km,n has a maximum matching of size min{m,n}. A complete bipartite graph Kn,n has a proper n-edge-coloring corresponding to a...