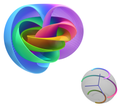
the Hopf invariant is a homotopy invariant of certain maps between n-spheres. In 1931 Heinz Hopf used Clifford parallels to construct the Hopf map η...

this time Hopf discovered the Hopf invariant of maps S 3 → S 2 {\displaystyle S^{3}\to S^{2}} and proved that the Hopf fibration has invariant 1. In the...

In differential topology, the Hopf fibration (also known as the Hopf bundle or Hopf map) describes a 3-sphere (a hypersphere in four-dimensional space)...

M^{4m+2}} (for m ≠ 0 , 1 , 3 {\displaystyle m\neq 0,1,3} ) and the mod 2 Hopf invariant of maps S 4 m + 2 + k → S 2 m + 1 + k {\displaystyle S^{4m+2+k}\to S^{2m+1+k}}...

The Hopf theorem (named after Heinz Hopf) is a statement in differential topology, saying that the topological degree is the only homotopy invariant of...

It is clear how to define a homotopy from [f][g] to [g][f]. Adams' Hopf invariant one theorem, named after Frank Adams, states that S0, S1, S3, S7 are...

1958 J. Frank Adams published a further generalization in terms of Hopf invariants on H-spaces which still limits the dimension to 1, 2, 4, or 8. It was...

differential point of view Hopf invariant – Homotopy invariant of maps between n-spheres Kissing number – Geometric concept Writhe – Invariant of a knot diagram...

S^{15}\hookrightarrow S^{31}\rightarrow S^{16},} the first non-trivial case of the Hopf invariant one problem, because such a fibration would imply that the failed relation...

classical case. He used this spectral sequence to attack the celebrated Hopf invariant one problem, which he completely solved in a 1960 paper by making a...

In complex geometry, a Hopf surface is a compact complex surface obtained as a quotient of the complex vector space (with zero deleted) C 2 ∖ { 0 } {\displaystyle...

In mathematical knot theory, the Hopf link is the simplest nontrivial link with more than one component. It consists of two circles linked together exactly...

In mathematics, the Hopf decomposition, named after Eberhard Hopf, gives a canonical decomposition of a measure space (X, μ) with respect to an invertible...

Princeton in 1955. His other collaborators included; J. Frank Adams (Hopf invariant problem), Jürgen Berndt (projective planes), Roger Bielawski (Berry–Robbins...

distinguished using a knot invariant, a "quantity" which is the same when computed from different descriptions of a knot. Important invariants include knot polynomials...

to coproducts, counits and antipodes of Hopf algebras. Since the Vassiliev invariants (or finite type invariants) are closely related to chord diagrams...

Reshetikhin–Turaev invariants (RT-invariants) are a family of quantum invariants of framed links. Such invariants of framed links also give rise to invariants of 3-manifolds...

Milnor invariants of length k + 1 are defined if all Milnor invariants of length less than or equal to k vanish. The first (2-fold) Milnor invariant is simply...

nontrivial example of a link with more than one component is called the Hopf link, which consists of two circles (or unknots) linked together once. The...

H_{n}(X;\mathbb {Z} ).} Fibration Hopf fibration Hopf invariant Knot theory Homotopy class Homotopy groups of spheres Topological invariant Homotopy group with coefficients...

One way to answer the question is using knot polynomials, which are invariants of the knot. If two diagrams have different polynomials, they represent...

to the Yang–Baxter equation (see § Basic properties); and in monodromy invariants of algebraic geometry. In this introduction let n = 4; the generalization...

In mathematics, and especially gauge theory, Seiberg–Witten invariants are invariants of compact smooth oriented 4-manifolds introduced by Edward Witten (1994)...

spheres" by R. Bott and J. Milnor and "On the nonexistence of elements of Hopf invariant one" by J. F. Adams". Bulletin of the American Mathematical Society...

appropriate Adem relations, was the solution by J. Frank Adams of the Hopf invariant one problem. One application of the mod 2 Steenrod algebra that is fairly...

structure of a Hopf algebra is when considering all H-modules as a category. The additional structure is also used to define invariant elements of an...

In the mathematical field of knot theory, a knot invariant is a quantity (in a broad sense) defined for each knot which is the same for equivalent knots...

They were introduced by J. Frank Adams (1960) in his solution to the Hopf invariant problem. Similarly, one can define tertiary cohomology operations from...

Topological K-theory has been applied in John Frank Adams’ proof of the “Hopf invariant one” problem via Adams operations. Adams also proved an upper bound...

In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander...