mathematics, Minkowski's first inequality for convex bodies is a geometrical result due to the German mathematician Hermann Minkowski. The inequality is closely...

inequality Melchior's inequality Milman's reverse Brunn–Minkowski inequality Milnor–Wood inequality Minkowski's first inequality for convex bodies Myers's theorem...

for example, a crescent shape, is not convex. The boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets...

known proofs of Brunn–Minkowski. The Brunn–Minkowski inequality gives much insight into the geometry of high dimensional convex bodies. In this section we...

English translation of Minkowski's paper, the Minkowski metric, as defined below, is referred to as the line element. The Minkowski inner product below appears...

"no" for every n ≥ 3. The solution of Shephard's problem requires Minkowski's first inequality for convex bodies and the notion of projection bodies of...

polytopes Minkowski sausage Minkowski island Minkowski snowflake Minkowski space (number field) Minkowski's bound Minkowski's first inequality for convex bodies...

In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined...

valuations on convex bodies inequalities and extremum problems convex functions and convex programs spherical and hyperbolic convexity Convex geometry is...

orthogonal projections of the convex bodies onto the axis are disjoint. The hyperplane separation theorem is due to Hermann Minkowski. The Hahn–Banach separation...

polytopes Minkowski's second theorem Minkowski space Minkowski's bound Minkowski's theorem in geometry of numbers Minkowski–Hlawka theorem Minkowski–Steiner...

Let C {\displaystyle C} be a smooth regular convex closed curve. Then the improved isoperimetric inequality states the following L 2 ⩾ 4 π A + 8 π | A...

K_{n})}}.} Numerous geometric inequalities, such as the Brunn–Minkowski inequality for convex bodies and Minkowski's first inequality, are special cases of the...

concept of manifold convergence. The Brunn–Minkowski inequality for the n-dimensional volumes of convex bodies K and L, v o l ( ( 1 − λ ) K + λ L ) 1 /...

boundary of a convex body in S⊥. Brunn–Minkowski inequality Prékopa–Leindler inequality Busemann, Herbert (1949). "A theorem on convex bodies of the Brunn-Minkowski...

a disk with radius w and perimeter 2πw. The Minkowski sum acts linearly on the perimeters of convex bodies, so the perimeter of K must be half the perimeter...

not defined by "entrywise" formulas. For instance, the Minkowski functional of a centrally-symmetric convex body in R n {\displaystyle \mathbb {R} ^{n}}...

polyhedron. A polytope may be convex. The convex polytopes are the simplest kind of polytopes, and form the basis for several different generalizations...

polyhedron. Analytically, such a convex polyhedron is expressed as the solution set for a system of linear inequalities. Defining polyhedra in this way...

space, then their Minkowski sum is approximately convex. It is named after mathematicians Lloyd Shapley and Jon Folkman, but was first published by the...

of inequalities Triangle inequality Bernoulli's inequality Cauchy–Schwarz inequality Hölder's inequality Minkowski inequality Jensen's inequality Chebyshev's...

to the properties of convex bodies. A convex polyhedron is called a zonotope if it is the Minkowski sum of segments. A convex body which is a limit of...

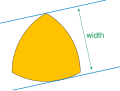
A convex body has constant width if and only if the Minkowski sum of the body and its 180° rotation is a circular disk; if so, the width of the body is...

of a convex body needed to cover the body, or equivalently the minimum number of light sources needed to illuminate the surface of the body; for instance...

Prékopa-Leindler inequality to other types of convex combinations of two positive functions. He strengthened the inequality and the Brunn-Minkowski inequality by introducing...

> 0 {\displaystyle c>0} . The reverse Brunn–Minkowski inequality states that for any pair of convex bodies K {\displaystyle K} and T {\displaystyle T}...

convex bodies with at most 2n smaller copies Solving the happy ending problem for arbitrary n {\displaystyle n} Improving lower and upper bounds for the...

sufficient for either exact or optimally approximate recovery of sufficiently sparse solutions. Their proofs, which involved the theory of convex duality...

of Yau's work are also seen in the mathematical and physical fields of convex geometry, algebraic geometry, enumerative geometry, mirror symmetry, general...

Yang, Deane; Zhang, Gaoyong (2000), "A new ellipsoid associated with convex bodies", Duke Mathematical Journal, 104 (3): 375–390, doi:10.1215/S0012-7094-00-10432-2...