In set theory, a paradoxical set is a set that has a paradoxical decomposition. A paradoxical decomposition of a set is two families of disjoint subsets...

well order any set allows certain constructions to be performed that have been called paradoxical. One example is the Banach–Tarski paradox, a theorem widely...

be self referential without being paradoxical ("This statement is written in English" is a true and non-paradoxical self-referential statement), self-reference...

discovery of paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox), various axiomatic systems were...

In mathematical logic, Russell's paradox (also known as Russell's antinomy) is a set-theoretic paradox published by the British philosopher and mathematician...

construction of such a paradoxical decomposition, based on earlier work by Giuseppe Vitali concerning the unit interval and on the paradoxical decompositions...

as a way to have set-like collections while differing from sets so as to avoid paradoxes, especially Russell's paradox (see § Paradoxes). The precise definition...

century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial...

{\displaystyle x\notin x} , it would state the existence of Russell's paradoxical set, giving a contradiction. It was this contradiction that led the axiom...

In set theory, the complement of a set A, often denoted by A c {\displaystyle A^{c}} (or A′), is the set of elements not in A. When all elements in the...

{Z} ,n=2k\}} The set of all even integers, expressed in set-builder notation. In mathematics and more specifically in set theory, set-builder notation...

the empty set or void set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero. Some axiomatic set theories...

without restriction, leads to paradoxes. One common example is Russell's paradox: there is no set consisting of "all sets that do not contain themselves"...

This is the paradoxical nature of Cantor's "paradox". While Cantor is usually credited with first identifying this property of cardinal sets, some mathematicians...

In computability theory, a set of natural numbers is computable (or decidable or recursive) if there is an algorithm that computes the membership of every...

other assumption is also disproved" leads to paradoxical consequences. Not to be confused with the Barber paradox. What the Tortoise Said to Achilles: If a...

In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations...

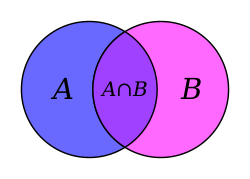
In set theory, the intersection of two sets A {\displaystyle A} and B , {\displaystyle B,} denoted by A ∩ B , {\displaystyle A\cap B,} is the set containing...

mathematics, an element (or member) of a set is any one of the distinct objects that belong to that set. For example, given a set called A containing the first four...

mathematics, an uncountable set, informally, is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related...

mathematical study of infinite sets began with Georg Cantor (1845–1918). This provided some counterintuitive facts and paradoxes. For example, the number line...

other paradoxes listed are difficult to interpret. "What the Tortoise Said to Achilles", written in 1895 by Lewis Carroll, describes a paradoxical infinite...

from the point of view of M, was seen as paradoxical in the early days of set theory; see Skolem's paradox for more. The minimal standard model includes...

a singleton (also known as a unit set or one-point set) is a set with exactly one element. For example, the set { 0 } {\displaystyle \{0\}} is a singleton...

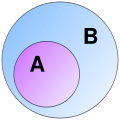
In mathematics, a set A is a subset of a set B if all elements of A are also elements of B; B is then a superset of A. It is possible for A and B to be...

the set of square numbers is countable, which was considered paradoxical for hundreds of years before modern set theory (see: § Pre-Cantorian Set theory)...

mathematics, the power set (or powerset) of a set S is the set of all subsets of S, including the empty set and S itself. In axiomatic set theory (as developed...

In set theory, an infinite set is a set that is not a finite set. Infinite sets may be countable or uncountable. The set of natural numbers (whose existence...

it to eliminate the very principle upon which that freedom relies is paradoxical. Michel Rosenfeld, in the Harvard Law Review in 1987, stated: "it seems...

therapists had been utilizing paradoxical treatments for a long time before the term was coined.: 133  Later on paradoxical intention was incorporated into...