versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial. Taylor's theorem is named...

denoted by the function Rn(x). Taylor's theorem can be used to obtain a bound on the size of the remainder. In general, Taylor series need not be convergent...

Wiles and Richard Taylor proved the modularity theorem for semistable elliptic curves, which was enough to imply Fermat's Last Theorem. Later, a series...

several results in mathematical analysis. Taylor's most famous developments are Taylor's theorem and the Taylor series, essential in the infinitesimal approach...

D = d d x {\displaystyle D={d \over dx}} is an operator version of Taylor's theorem — and is therefore only valid under caveats about f being an analytic...

The version of Taylor's theorem that expresses the error term as an integral can be seen as a generalization of the fundamental theorem. There is a version...

the infinitely small quantities he used. He was the first to prove Taylor's theorem rigorously, establishing his well-known form of the remainder. He wrote...

Rolle's theorem is used to prove the mean value theorem, of which Rolle's theorem is indeed a special case. It is also the basis for the proof of Taylor's theorem...

value theorem Differential equation Differential operator Newton's method Taylor's theorem L'Hôpital's rule General Leibniz rule Mean value theorem Logarithmic...

mathematical analysis, the Whitney extension theorem is a partial converse to Taylor's theorem. Roughly speaking, the theorem asserts that if A is a closed subset...

In multivariable calculus, the implicit function theorem is a tool that allows relations to be converted to functions of several real variables. It does...

theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls, or simply the curl theorem,...

a neighborhood U of the point x 0 {\displaystyle x_{0}} . Then by Taylor's theorem, f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + ⋯ + f ( k ) ( x 0...

Taylor's of Loughborough, or Taylor's, in England Taylor Company, a maker of foodservice equipment owned by Middleby Corporation Taylor's theorem, in...

Taylor's theorem that falls between the limits a and b A number used in error approximations for formulas that are applications of Taylor's theorem,...

formulas. Taylor's theorem gives a precise bound on how good the approximation is. If f is a polynomial of degree less than or equal to d, then the Taylor polynomial...

named after Jacques Hadamard, is essentially a first-order form of Taylor's theorem, in which we can express a smooth, real-valued function exactly in...

this case, they are also called indefinite integrals. The fundamental theorem of calculus relates definite integration to differentiation and provides...

In mathematics, the mean value theorem (or Lagrange's mean value theorem) states, roughly, that for a given planar arc between two endpoints, there is...

curves. These two branches are related to each other by the fundamental theorem of calculus. They make use of the fundamental notions of convergence of...

distributed. The characteristic function of Y 1 {\textstyle Y_{1}} is, by Taylor's theorem, φ Y 1 ( t n ) = 1 − t 2 2 n + o ( t 2 n ) , ( t n ) → 0 {\displaystyle...

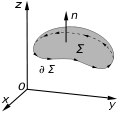
generalized Stokes theorem (sometimes with apostrophe as Stokes' theorem or Stokes's theorem), also called the Stokes–Cartan theorem, is a statement about...

Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law...

the chain rule if the derivative is permitted to be discontinuous.) (Taylor's theorem with remainder) Suppose that the line segment between u ∈ U {\displaystyle...

In mathematics, the inverse function theorem is a theorem that asserts that, if a real function f has a continuous derivative near a point where its derivative...

In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D (surface in R...

mathematics, the Milliken–Taylor theorem in combinatorics is a generalization of both Ramsey's theorem and Hindman's theorem. It is named after Keith Milliken...

In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem relating the flux of a vector field through...

statistician Wassily Hoeffding. The proof of Hoeffding's lemma uses Taylor's theorem and Jensen's inequality. Hoeffding's lemma is itself used in the proof...

when h is small. The error in this approximation can be derived from Taylor's theorem. Assuming that f is twice differentiable, we have Δ h [ f ] ( x ) h...