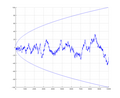
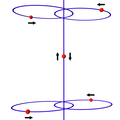
In the branch of mathematics called knot theory, the volume conjecture is an open problem that relates quantum invariants of knots to the hyperbolic geometry...

In the geometry of numbers, Ehrhart's volume conjecture gives an upper bound on the volume of a convex body containing only one lattice point in its interior...

odd r {\displaystyle r} , in 2018 Q. Chen and T. Yang suggested the volume conjecture for the RT-invariants, which essentially says that the RT-invariants...

In mathematics, Thurston's geometrization conjecture (now a theorem) states that each of certain three-dimensional topological spaces has a unique geometric...

2000, six remain unsolved to date: Birch and Swinnerton-Dyer conjecture Hodge conjecture Navier–Stokes existence and smoothness P versus NP Riemann hypothesis...

infinity, the limit value would give the hyperbolic volume of the knot complement. (See Volume conjecture.) In 2000 Mikhail Khovanov constructed a certain...

The Kepler conjecture, named after the 17th-century mathematician and astronomer Johannes Kepler, is a mathematical theorem about sphere packing in three-dimensional...

unsolved mathematical problems, the Birch and Swinnerton-Dyer conjecture, Hodge conjecture, Navier–Stokes existence and smoothness, P versus NP problem...

In the mathematical field of geometric topology, the Poincaré conjecture (UK: /ˈpwæ̃kæreɪ/, US: /ˌpwæ̃kɑːˈreɪ/, French: [pwɛ̃kaʁe]) is a theorem about...

analysis of Ricci flow, and proved the Poincaré conjecture and Thurston's geometrization conjecture, the former of which had been a famous open problem...

preprint "Volume estimates for unions of convex sets, and the Kakeya set conjecture in three dimensions" claiming to solve the Kakeya conjecture in three...

The abc conjecture (also known as the Oesterlé–Masser conjecture) is a conjecture in number theory that arose out of a discussion of Joseph Oesterlé and...

In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, b,...

spheres. He conjectured in 1943 that the minimal volume of any cell in the resulting Voronoi decomposition was at least as large as the volume of a regular...

Mahler volume are the balls and solid ellipsoids; this is now known as the Blaschke–Santaló inequality. The still-unsolved Mahler conjecture states that...

Hong Wang; Joshua Zahl (2025-02-24). "Volume estimates for unions of convex sets, and the Kakeya set conjecture in three dimensions". arXiv:2502.17655...

{e^{n+1}}{\sqrt {2\pi n}}}.} Ehrhart's volume conjecture is that this is the (optimal) upper bound on the volume of a convex body containing only one lattice...

geometry. His contributions include his solution of the Grothendieck conjecture in anabelian geometry about hyperbolic curves over number fields. Mochizuki...

In complex analysis, de Branges's theorem, or the Bieberbach conjecture, is a theorem that gives a necessary condition on a holomorphic function in order...

the proof. The Poincaré conjecture and the spherical space form conjecture are corollaries of the geometrization conjecture, although there are shorter...

Novikov conjecture is one of the most important unsolved problems in topology. It is named for Sergei Novikov who originally posed the conjecture in 1965...

In mathematics, the Mertens conjecture is the statement that the Mertens function M ( n ) {\displaystyle M(n)} is bounded by ± n {\displaystyle \pm {\sqrt...

In mathematics, Sendov's conjecture, sometimes also called Ilieff's conjecture, concerns the relationship between the locations of roots and critical...

This fact and useful properties of alternating knots, such as the Tait conjectures, was what enabled early knot tabulators, such as Tait, to construct tables...

Shinsei Ryu and Tadashi Takayanagi published 2006 a conjecture within holography that posits a quantitative relationship between the entanglement entropy...

In mathematics, homological conjectures have been a focus of research activity in commutative algebra since the early 1960s. They concern a number of...

zero-divisor conjecture implies the idempotent conjecture and is implied by the unit conjecture. As of 2021, the zero divisor and idempotent conjectures are open...

In mathematics, Serre's modularity conjecture, introduced by Jean-Pierre Serre (1975, 1987), states that an odd, irreducible, two-dimensional Galois representation...

In mathematics, the Sato–Tate conjecture is a statistical statement about the family of elliptic curves Ep obtained from an elliptic curve E over the rational...

In physics, the Painlevé conjecture is a theorem about singularities among the solutions to the n-body problem: there are noncollision singularities for n ≥ 4...