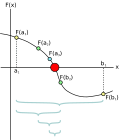
the bisection method is a root-finding method that applies to any continuous function for which one knows two values with opposite signs. The method consists...

called the regula falsi method, is similar to the bisection method, but instead of using bisection search's middle of the interval it uses the x-intercept...

regula-falsi and bisection that achieves optimal worst-case and asymptotic guarantees. The idea to combine the bisection method with the secant method goes back...

The method of bisection avoids this hypothetical convergence problem. Though regula falsi always converges, usually considerably faster than bisection, there...

performance of the bisection method. It is also the first method with guaranteed average performance strictly better than the bisection method under any continuous...

polynomial (see Properties of polynomial roots for such bounds). The bisection method consists roughly of starting from an interval containing all real roots...

process again return None # Newton's method did not converge Aitken's delta-squared process Bisection method Euler method Fast inverse square root Fisher scoring...

tools allow specific changesets to be ignored during a bisection search. Although the bisection method can be completed manually, one of its main advantages...

one can employ standard root-finding algorithms like the bisection method or Newton's method. Roots of F {\displaystyle F} and solutions to the boundary...

center-of-gravity method is a theoretic algorithm for convex optimization. It can be seen as a generalization of the bisection method from one-dimensional...

is available, then the maximum power point can be obtained using a bisection method. When directly connecting a load to cell, the operating point of the...

two equal parts Bisection method, a root-finding algorithm Equidistant set Bisect (philately), the use of postage stamp halves Bisector (music), a half...

method. As an example, consider the problem of solving 3x3 + 4 = 28 for the unknown quantity x. For the iterative method, apply the bisection method to...

converge. The secant method does not require or guarantee that the root remains bracketed by sequential iterates, like the bisection method does, and hence...

for the maximum (minimum) of a unimodal function in an interval. The Bisection method is a similar algorithm for finding a zero of a function. Note that...

from the original on 20 April 2016. Retrieved 1 May 2016. "8.6. bisect — Array bisection algorithm". The Python Standard Library. Python Software Foundation...

mathematics-based methods. Adams' method (differential equations) Akra–Bazzi method (asymptotic analysis) Bisection method (root finding) Brent's method (root finding)...

eigenvectors) can be computed numerically in time O(n log(n)), using bisection on the characteristic polynomial. Iterative algorithms solve the eigenvalue...

(and smaller) width, a method known as mincing. This then avoids the calculations for intermediate bisection steps. Both methods are only suitable for...

that we can evaluate not only f but also its derivative.: sec.5  The bisection method computes the derivative of f at the center of the interval, c: if f'(c)=0...

the conditional distribution equals a predefined entropy using the bisection method. As a result, the bandwidth is adapted to the density of the data:...

Muller's method, but interpolates the inverse Brent's method — combines bisection method, secant method and inverse quadratic interpolation Ridders' method —...

continued fractions method, or by bisection, leading to (among others) the Vincent–Collins–Akritas (VCA) bisection method. The "bisection part" of this all...

{\displaystyle \xi ^{\ast }\in \mathbb {R} } can be found through the bisection method since in most regular models, such as the aforementioned generalized...

Newton's method makes no guarantees on stability), or, alternatively, use a bracketing solver such as the bisection method or the Brent method, which are...

implemented and are available in Mathematica (continued fraction method) and Maple (bisection method), as well as in other main computer algebra systems (SageMath...

the four bisections, to which the viewer’s attention will be drawn. However, the DM is very strict about placing details exactly on the bisection, allowing...

use a numerical root-finding algorithm such as the bisection method to invert the cdf. Other methods rely on an approximation of the inverse via interpolation...

extending the idea of enclosing roots like in the one-dimensional bisection method to the complex plane. It uses the Schur-Cohn test to test increasingly...

Newton-Raphson, secant, or regula falsi numerically unstable. In that case, the bisection method will provide guaranteed convergence, particularly since the solution...