question marks, boxes, or other symbols. In mathematical set theory, Cantor's theorem is a fundamental result which states that, for any set A {\displaystyle...

numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of. Originally, Cantor's theory of transfinite numbers...

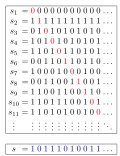
R. A generalized form of the diagonal argument was used by Cantor to prove Cantor's theorem: for every set S, the power set of S—that is, the set of all...

In set theory, Cantor's paradox states that there is no set of all cardinalities. This is derived from the theorem that there is no greatest cardinal...

The theorem is named after Felix Bernstein and Ernst Schröder. It is also known as the Cantor–Bernstein theorem or Cantor–Schröder–Bernstein theorem, after...

philosophers. Cantor's theorem implies that there are sets having cardinality greater than the infinite cardinality of the set of natural numbers. Cantor's argument...

mathematics and logic, such as Cantor's diagonal argument, Cantor's theorem, Russell's paradox, Gödel's first incompleteness theorem, Turing's solution to the...

Cantor's intersection theorem, also called Cantor's nested intervals theorem, refers to two closely related theorems in general topology and real analysis...

Cantor's first set theory article contains Georg Cantor's first theorems of transfinite set theory, which studies infinite sets and their properties. One...

Look up Cantor's theorem in Wiktionary, the free dictionary. Cantor's theorem is a fundamental result in mathematical set theory. Cantor's theorem may also...

Heine–Cantor theorem states that a continuous function between two metric spaces is uniformly continuous if its domain is compact. The theorem is named...

class. Zermelo's paper may be the first to mention the name "Cantor's theorem". Cantor's theorem: "If M is an arbitrary set, then always M < P(M) [the power...

of all sets, provided that both exist. However, this conflicts with Cantor's theorem that the power set of any set (whether infinite or not) always has...

the power set must be larger than the original set). In particular, Cantor's theorem shows that the power set of a countably infinite set is uncountably...

following theorems: Cantor's diagonal argument (the earliest) Cantor's theorem Russell's paradox Diagonal lemma Gödel's first incompleteness theorem Tarski's...

Gödel's incompleteness theorems are two theorems of mathematical logic that are concerned with the limits of provability in formal axiomatic theories...

sets. Cantor gave two proofs that the cardinality of the set of integers is strictly smaller than that of the set of real numbers (see Cantor's first...

Burnside's lemma Cantor's theorem Cantor–Bernstein–Schroeder theorem Cayley's formula Cayley's theorem Clique problem (to do) Compactness theorem (very compact...

must satisfy the sentence saying the real numbers are uncountable. Cantor's theorem states that some sets are uncountable. This counterintuitive situation...

Cantor proved that the real numbers were uncountable; in 1891, he proved by his diagonal argument the more general result known as Cantor's theorem:...

In order theory and model theory, branches of mathematics, Cantor's isomorphism theorem states that every two countable dense unbounded linear orders are...

This theorem is proved using Cantor's first uncountability proof, which differs from the more familiar proof using his diagonal argument. Cantor introduced...

{P}}(A)} . A proof is given in the article Cantor's theorem. As an immediate consequence of this and the Basic Theorem above we have: Proposition—The set P...

algorithm to solve any first-order problem in Euclidean geometry. Cantor's theorem Artin, Emil (1988) [1957], Geometric Algebra, Wiley Classics Library...

\kappa } . Thus, Kőnig's theorem gives us an alternate proof of Cantor's theorem. (Historically of course Cantor's theorem was proved much earlier.)...

number, Cantor–Bernstein–Schroeder theorem, Cantor's diagonal argument, Cantor's first uncountability proof, Cantor's theorem, well-ordering theorem, axiom...

paradox in type theory Basic Law V Cantor's diagonal argument – Proof in set theory Gödel's incompleteness theorems – Limitative results in mathematical...

{2}}} . By a theorem of L. E. J. Brouwer, this is equivalent to being perfect, nonempty, compact, metrizable and zero-dimensional. The Cantor ternary set...

universal set, so it must be that Cantor's theorem (in its original form) does not hold in NF. Indeed, the proof of Cantor's theorem uses the diagonalization argument...

of infinite sets, the behavior is more complex. A fundamental theorem due to Georg Cantor shows that it is possible for two infinite sets to have different...