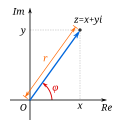
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions...

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematics that investigates functions of complex...

In mathematics (particularly in complex analysis), the argument of a complex number z, denoted arg(z), is the angle between the positive real axis and...

That all holomorphic functions are complex analytic functions, and vice versa, is a major theorem in complex analysis. Holomorphic functions are also sometimes...

In complex analysis, a branch of mathematics, Bloch's theorem describes the behaviour of holomorphic functions defined on the unit disk. It gives a lower...

In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along...

mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function...

In complex analysis, Liouville's theorem, named after Joseph Liouville (although the theorem was first proven by Cauchy in 1844), states that every bounded...

most natural proofs for statements in real analysis or even number theory employ techniques from complex analysis (see prime number theorem for an example)...

mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane. Contour integration...

distinguished from complex analysis, which deals with the study of complex numbers and their functions. The theorems of real analysis rely on the properties...

In mathematics and in particular the field of complex analysis, Hurwitz's theorem is a theorem associating the zeroes of a sequence of holomorphic, compact...

This is a glossary of concepts and results in real analysis and complex analysis in mathematics. In particular, it includes those in measure theory (as...

real and complex numbers and functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be...

by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes called the Argand plane or Gauss plane. In complex analysis, the complex...

{\displaystyle 0} is near to very small numbers. The extended complex numbers are useful in complex analysis because they allow for division by zero in some circumstances...

In complex analysis, the open mapping theorem states that if U {\displaystyle U} is a domain of the complex plane C {\displaystyle \mathbb {C} } and f...

Fourier Analysis: An Introduction; Complex Analysis; Real Analysis: Measure Theory, Integration, and Hilbert Spaces; and Functional Analysis: Introduction...

theorem (complex analysis) Carleson–Jacobs theorem (complex analysis) Carlson's theorem (complex analysis) Cauchy integral theorem (complex analysis) Cauchy–Hadamard...

complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis...

Feminism. New York: Vintage Books. ISBN 9780394714424. Tobin, B. (1988). Reverse Oedipal Complex Analysis. New York: Random House Publishing Company....

ISBN 978-0-521-48364-3 Rao, Murali; Stetkær, Henrik (1991). Complex Analysis: An Invitation : a Concise Introduction to Complex Function Theory. World Scientific. p. 113...

Analysis (pl.: analyses) is the process of breaking a complex topic or substance into smaller parts in order to gain a better understanding of it. The...

In complex analysis (a branch of mathematics), a pole is a certain type of singularity of a complex-valued function of a complex variable. It is the simplest...

boundary. In complex analysis, a complex domain (or simply domain) is any connected open subset of the complex plane C. For example, the entire complex plane...

1912 – April 3, 1986) was an Israeli mathematician specializing in complex analysis. Over the course of his work at the Technion he was the Dean of the...

heading. As in complex analysis of functions of one variable, which is the case n = 1, the functions studied are holomorphic or complex analytic so that...

November 1992) was a Japanese mathematician working in the field of complex analysis. He was the founder of the Japanese Association of Mathematical Sciences...

In mathematics, in the branch of complex analysis, a holomorphic function on an open subset of the complex plane is called univalent if it is injective...

the partial derivatives and directional derivatives exist. In complex analysis, complex-differentiability is defined using the same definition as single-variable...