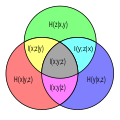
particularly information theory, the conditional mutual information is, in its most basic form, the expected value of the mutual information of two random...

In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two...

In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable Y {\displaystyle...

interpretation in algebraic topology. The conditional mutual information can be used to inductively define the interaction information for any finite number of variables...

)}{\bigr ]}\end{aligned}}} The score uses the conditional mutual information and the mutual information to estimate the redundancy between the already...

generalization of quantities of information to continuous distributions), and the conditional mutual information. Also, pragmatic information has been proposed as...

of the information content of random variables and a measure over sets. Namely the joint entropy, conditional entropy, and mutual information can be considered...

expressed as special cases of a single inequality involving the conditional mutual information, namely I ( A ; B | C ) ≥ 0 , {\displaystyle I(A;B|C)\geq 0...

entropy measures such as Rényi entropy. Transfer entropy is conditional mutual information, with the history of the influenced variable Y t − 1 : t − L...

( A : B | Λ ) {\displaystyle S(A:B|\Lambda )} , the quantum Conditional Mutual Information (CMI), below. A more general version of Eq.(1) replaces the...

Redundancy (information theory). The characterization here imposes an additive property with respect to a partition of a set. Meanwhile, the conditional probability...

measures of information: entropy, joint entropy, conditional entropy and mutual information. Information diagrams are a useful pedagogical tool for teaching...

or source information rate is a function assigning an entropy to a stochastic process. For a strongly stationary process, the conditional entropy for...

method Logistic regression Conditional entropy Kullback–Leibler distance Maximum-likelihood estimation Mutual information Perplexity Thomas M. Cover,...

i | Y i − 1 ) {\displaystyle I(X^{i};Y_{i}|Y^{i-1})} is the conditional mutual information I ( X 1 , X 2 , . . . , X i ; Y i | Y 1 , Y 2 , . . . , Y i...

Z {\displaystyle Z} are conditionally independent, given Y {\displaystyle Y} , which means the conditional mutual information, I ( X ; Z ∣ Y ) = 0 {\displaystyle...

of the channel, as defined above, is given by the maximum of the mutual information between the input and output of the channel, where the maximization...

(Y|X)+\mathrm {H} (X)} . Joint entropy is also used in the definition of mutual information: 21  I ⁡ ( X ; Y ) = H ( X ) + H ( Y ) − H ( X , Y ) {\displaystyle...

{\displaystyle X} , and I Q ( Y ; X ) {\displaystyle I_{Q}(Y;X)} is the mutual information between Y {\displaystyle Y} and X {\displaystyle X} defined as I (...

In information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified...

The differential analogies of entropy, joint entropy, conditional entropy, and mutual information are defined as follows: h ( X ) = − ∫ X f ( x ) log ⁡...

In information theory, Shannon's source coding theorem (or noiseless coding theorem) establishes the statistical limits to possible data compression for...

In information theory, the limiting density of discrete points is an adjustment to the formula of Claude Shannon for differential entropy. It was formulated...

package for computing all information distances and volumes, multivariate mutual information, conditional mutual information, joint entropies, total correlations...

{\displaystyle I_{P}:=-\ln \mu (P(x))} Similarly, the conditional information of partition P {\textstyle P} , conditional on partition Q {\textstyle Q} , about x {\textstyle...

classical intuition, except that quantum conditional entropies can be negative, and quantum mutual informations can exceed the classical bound of the marginal...

In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption...

trees, the term is sometimes used synonymously with mutual information, which is the conditional expected value of the Kullback–Leibler divergence of...

In information theory and communication, the Slepian–Wolf coding, also known as the Slepian–Wolf bound, is a result in distributed source coding discovered...

significance as a measure of discrete information since it is actually the limit of the discrete mutual information of partitions of X {\displaystyle X}...