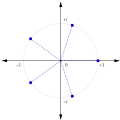
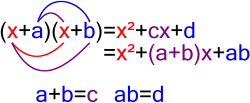In mathematics, the nth cyclotomic polynomial, for any positive integer n, is the unique irreducible polynomial with integer coefficients that is a divisor...

geometric fact accounts for the term "cyclotomic" in such phrases as cyclotomic field and cyclotomic polynomial; it is from the Greek roots "cyclo" (circle)...

of certain integer values of the cyclotomic polynomials. Because cyclotomic polynomials are irreducible polynomials over the integers, such a factorization...

important class of polynomials whose irreducibility can be established using Eisenstein's criterion is that of the cyclotomic polynomials for prime numbers...

unity. Then the minimal polynomial of ζ n {\displaystyle \zeta _{n}} is given by the n {\displaystyle n} -th cyclotomic polynomial Φ n ( x ) {\displaystyle...

irreducible cyclotomic polynomials", Electronics and Communications in Japan, 74 (4): 106–113, doi:10.1002/ecjc.4430740412, MR 1136200. all one polynomial at PlanetMath...

denominator, 1 − z j, which is the product of cyclotomic polynomials. The left hand side of the cyclotomic identity is the generating function for the free...

by ζ n {\displaystyle \zeta _{n}} . The n {\displaystyle n} th cyclotomic polynomial Φ n ( x ) = ∏ gcd ( k , n ) = 1 1 ≤ k ≤ n ( x − e 2 π i k / n )...

of palindromic polynomials include cyclotomic polynomials and Eulerian polynomials. If a is a root of a polynomial that is either palindromic or antipalindromic...

{\displaystyle n} th cyclotomic polynomial are distinct in every field of characteristic p {\displaystyle p} , as this polynomial is a divisor of X n −...

number i is X 2 + 1 {\displaystyle X^{2}+1} . The cyclotomic polynomials are the minimal polynomials of the roots of unity. In linear algebra, the n×n...

All-one polynomials Abel polynomials Bell polynomials Bernoulli polynomials Cyclotomic polynomials Dickson polynomials Fibonacci polynomials Lagrange...

class of examples comes from the splitting fields of cyclotomic polynomials. These are polynomials Φ n {\displaystyle \Phi _{n}} defined as Φ n ( x ) =...

those associated with the cyclotomic polynomials of degrees 5 and 17. Charles Hermite, on the other hand, showed that polynomials of degree 5 are solvable...

evidence it is not known that this sequence extends indefinitely. The cyclotomic polynomials Φ k ( x ) {\displaystyle \Phi _{k}(x)} for k = 1 , 2 , 3 , … {\displaystyle...

not divide n, and Q n ( x ) {\displaystyle Q_{n}(x)} is the nth cyclotomic polynomial. For example, a 6 − b 6 = Q ¯ 1 ( a , b ) Q ¯ 2 ( a , b ) Q ¯ 3...

function φ(n) in number theory; also called Euler's phi function. The cyclotomic polynomial functions Φn(x) of algebra. The number of electrical phases in a...

mathematician and educator. Her research focused on the area of cyclotomic polynomials. Beiter was born in Buffalo to Kathryn (née Kiel) and Edward Frederick...

{\displaystyle x^{n}-1=0} for any n, and the equations defined by cyclotomic polynomials, all of whose solutions can be expressed in radicals. Abel's proof...

2, the polynomial Φ(x) will be the cyclotomic polynomial xn + 1. Other choices of n are possible but the corresponding cyclotomic polynomials are more...

prime Emma Lehmer, "On the magnitude of the coefficients of the cyclotomic polynomial", Bulletin of the American Mathematical Society 42 (1936), no. 6...

measure of an irreducible non-cyclotomic polynomial. Lehmer's polynomial is a factor of the shorter degree-12 polynomial, Q ( x ) = x 12 − x 7 − x 6 −...

Brahmagupta polynomials Caloric polynomial Charlier polynomials Chebyshev polynomials Chihara–Ismail polynomials Cyclotomic polynomials Dickson polynomial Ehrhart...

primality test (also known as Agrawal–Kayal–Saxena primality test and cyclotomic AKS test) is a deterministic primality-proving algorithm created and published...

divisors of n and Φ d ( x ) {\displaystyle \Phi _{d}(x)} is the d-th cyclotomic polynomial, and x n − 1 x − 1 = ∑ i = 0 n − 1 x i = 1 + x + ⋯ + x n − 1 {\displaystyle...

the fourth cyclotomic polynomial. As with the cyclotomic polynomials more generally, Φ 4 {\displaystyle \Phi _{4}} is an irreducible polynomial, so this...

Equivalently, a regular n-gon is constructible if any root of the nth cyclotomic polynomial is constructible. Restating the Gauss–Wantzel theorem: A regular...

identity for polynomials. x n − 1 = ∏ d | n Φ d ( x ) {\displaystyle x^{n}-1=\prod _{d|n}\Phi _{d}(x)} , a product of cyclotomic polynomials. Factoring...

{Q} )} . The minimal polynomials in Q[x] of roots of unity are the cyclotomic polynomials. The roots of the minimal polynomial of 2cos(2π/n) are twice...

irreducibility criterion. Finally, it can be used to show that cyclotomic polynomials (unitary units with integer coefficients) are irreducible. Gauss's...