mathematics, the Fibonacci polynomials are a polynomial sequence which can be considered as a generalization of the Fibonacci numbers. The polynomials generated...

golden ratio, Zeckendorf representations, Binet forms, Fibonacci polynomials, and Chebyshev polynomials. However, many other topics, especially as related...

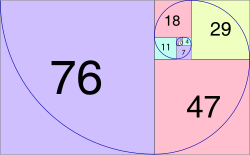
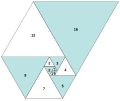
the Fibonacci sequence is a sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence...

The Chebyshev polynomials are two sequences of orthogonal polynomials related to the cosine and sine functions, notated as T n ( x ) {\displaystyle T_{n}(x)}...

In mathematics, the Fibonacci numbers form a sequence defined recursively by: F n = { 0 n = 0 1 n = 1 F n − 1 + F n − 2 n > 1 {\displaystyle...

Brahmagupta–Fibonacci identity Fibonacci coding Fibonacci cube Fibonacci heap Fibonacci polynomials Fibonacci prime Fibonacci pseudoprime Fibonacci quasicrystal...

All-one polynomials Abel polynomials Bell polynomials Bernoulli polynomials Cyclotomic polynomials Dickson polynomials Fibonacci polynomials Lagrange...

calculations of pentagons and decagons; his writings influenced that of Fibonacci (Leonardo of Pisa) (c. 1170–1250), who used the ratio in related geometry...

Ehrhart polynomial Exponential polynomials Favard's theorem Fibonacci polynomials Gegenbauer polynomials Hahn polynomials Hall–Littlewood polynomials Heat...

−1) : Fibonacci polynomials Vn(x, −1) : Lucas polynomials Un(2x, 1) : Chebyshev polynomials of second kind Vn(2x, 1) : Chebyshev polynomials of first...

way as Fibonacci polynomials are derived from the Fibonacci numbers, the Lucas polynomials L n ( x ) {\displaystyle L_{n}(x)} are a polynomial sequence...

^{7}-x^{6}-x^{5}+x^{2}+x+1.\end{aligned}}} The cyclotomic polynomials are monic polynomials with integer coefficients that are irreducible over the field...

above, Dickson polynomials are Lucas sequences. Specifically, for α = −1, the Dickson polynomials of the first kind are Fibonacci polynomials, and Dickson...

require a long carry chain). The table of primitive polynomials shows how LFSRs can be arranged in Fibonacci or Galois form to give maximal periods. One can...

mathematics Brahmagupta polynomials List of Indian mathematicians List of Italian mathematicians Sum of two squares theorem "Brahmagupta-Fibonacci Identity". Marc...

conditions hold: 2p−1 ≡ 1 (mod p), f(1)p+1 ≡ 0 (mod p), f(x)k is the k-th Fibonacci polynomial at x. Selfridge, Carl Pomerance and Samuel Wagstaff together offer...

– 17 January 2000) was a French mathematician who introduced Ehrhart polynomials in the 1960s. Ehrhart received his high school diploma at the age of...

cubic polynomials.[citation needed] It is not locally connected. This property is inherited by the connectedness locus of real cubic polynomials.[citation...

Iterated function Lagged Fibonacci generator Master theorem (analysis of algorithms) Mathematical induction Orthogonal polynomials Recursion Recursion (computer...

number of primitive polynomials of degree 25 over GF(2) 1,299,709 = 100,000th prime number 1,336,336 = 11562 = 344 1,346,269 = Fibonacci number, Markov number...

Gaussian binomial coefficients (also called Gaussian coefficients, Gaussian polynomials, or q-binomial coefficients) are q-analogs of the binomial coefficients...

} In a similar way to the Fibonacci numbers that can be generalized to a set of polynomials called the Fibonacci polynomials, the Padovan sequence numbers...

algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian...

A Lagged Fibonacci generator (LFG or sometimes LFib) is an example of a pseudorandom number generator. This class of random number generator is aimed...

It is one of several graph polynomials studied in algebraic graph theory. Several different types of matching polynomials have been defined. Let G be...

defined with respect to polynomials of degree at least 2, but they have been most extensively studied in the case of quadratic polynomials. The definition of...

±2759640, in which cases the polynomial is reducible. As solving reducible quintic equations reduces immediately to solving polynomials of lower degree, only...

689212 = 16813 = 416 4,807,526,976 = 48th Fibonacci number. 4,822,382,628 = number of primitive polynomials of degree 38 over GF(2) 4,984,209,207 = 875...

number of primitive polynomials of degree 22 over GF(2) 120,284 = Keith number 120,960 = highly totient number 121,393 = Fibonacci number 123,717 = smallest...

this case is the Fibonacci sequence, which has constant coefficients a n = b n = 1 {\displaystyle a_{n}=b_{n}=1} . Orthogonal polynomials Pn all have a TTRR...