In mathematics and computer programming, index notation is used to specify the elements of an array of numbers. The formalism of how indices are used varies...

Multi-index notation is a mathematical notation that simplifies formulas used in multivariable calculus, partial differential equations and the theory...

Abstract index notation (also referred to as slot-naming index notation) is a mathematical notation for tensors and spinors that uses indices to indicate...

implies summation over a set of indexed terms in a formula, thus achieving brevity. As part of mathematics it is a notational subset of Ricci calculus; however...

In mathematics, Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields on a differentiable manifold, with...

referred to as scientific form or standard index form, or standard form in the United Kingdom. This base ten notation is commonly used by scientists, mathematicians...

associated names for this idea: Mandel notation, Mandel–Voigt notation and Nye notation are others found. Kelvin notation is a revival by Helbig of old ideas...

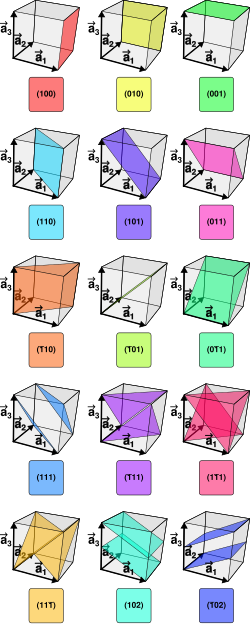
Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices. In particular, a family of lattice planes of...

a chemical symbol is used, e.g. "C" for carbon, standard notation (now known as "AZE notation" because A is the mass number, Z the atomic number, and E...

value of the function f at the point (x0, t0). Index notation may be used instead of functional notation. That is, instead of writing f (x), one writes...

}(dy\wedge dz)&=dt\wedge dx\,.\end{aligned}}} These are summarized in the index notation as ⋆ ( d x μ ) = η μ λ ε λ ν ρ σ 1 3 ! d x ν ∧ d x ρ ∧ d x σ , ⋆ ( d...

abstract index notation is a way to write tensors such that the indices are no longer thought of as numerical, but rather are indeterminates. This notation captures...

general contraction operation is sometimes called the trace. In tensor index notation, the basic contraction of a vector and a dual vector is denoted by f...

of tensor theory – tensor index notation. Order of a tensor The components of a tensor with respect to a basis is an indexed array. The order of a tensor...

given. Then any alternating tensor t ∈ Ar(V) ⊂ Tr(V) can be written in index notation with the Einstein summation convention as t = t i 1 i 2 ⋯ i r e i 1...

lower case epsilon ε or ϵ, or less commonly the Latin lower case e. Index notation allows one to display permutations in a way compatible with tensor analysis:...

Antisymmetric permutation object acting on tensors Ricci calculus – Tensor index notation for tensor-based calculations Symmetric tensor – Tensor invariant under...

In mathematics and physics, Penrose graphical notation or tensor diagram notation is a (usually handwritten) visual depiction of multilinear functions...

matrix A by producing another matrix, often denoted by AT (among other notations). The transpose of a matrix was introduced in 1858 by the British mathematician...

bundle – Construction in differential topology Ricci calculus – Tensor index notation for tensor-based calculations Spinor field – Geometric structurePages...

or no columns, called an empty matrix. The specifics of symbolic matrix notation vary widely, with some prevailing trends. Matrices are commonly written...

Einstein summation notation: any index may appear at most twice and furthermore a raised index must contract with a lowered index. With these rules we...

mathematics, the wedge notation a ∧ b is often used (in conjunction with the name vector product), although in pure mathematics such notation is usually reserved...

substituting by 1 the extra variable. The multi-index notation is often useful for having a compact notation, specially when there are more than two or three...

the noncommutativity of the second covariant derivative. In abstract index notation, R d c a b Z c = ∇ a ∇ b Z d − ∇ b ∇ a Z d . {\displaystyle R^{d}{}_{cab}Z^{c}=\nabla...

g_{\rho \sigma }.} The metric tensor plays a key role in index manipulation. In index notation, the coefficients g μ ν {\displaystyle g_{\mu \nu }} of...

linearly dependent is zero. A common notation for the wedge product of elementary k-forms is so called multi-index notation: in an n-dimensional context, for...

ones mixed. Notationally, these tensors differ from each other by the covariance/contravariance of their indices. A given contravariant index of a tensor...

coordinate-free language and using a local coordinate system and the traditional index notation. The covariant derivative of a tensor field is presented as an extension...

}F_{\beta \gamma }+\partial _{\beta }F_{\gamma \alpha }=0} or using the index notation with square brackets[note 1] for the antisymmetric part of the tensor:...