} are singular). Lebesgue's decomposition theorem can be refined in a number of ways. First, as the Lebesgue-Radon-Nikodym theorem. That is, let ( Ω...

+ ih is the required function. Lebesgue's decomposition theorem shows that the assumptions of the Radon–Nikodym theorem can be found even in a situation...

In physics and mathematics, the Helmholtz decomposition theorem or the fundamental theorem of vector calculus states that certain differentiable vector...

Lebesgue covering dimension Lebesgue constants Lebesgue's decomposition theorem Lebesgue's density theorem Lebesgue differentiation theorem Lebesgue integration...

measure Helmholtz decomposition, decomposition of a vector field Indecomposable continuum Lebesgue's decomposition theorem, decomposition of a measure Lie...

mathematics the monotone convergence theorem usually refers to a fundamental result in measure theory due to Lebesgue and Beppo Levi that says that for sequences...

integrable functions. In higher dimensions Lebesgue's differentiation theorem generalizes the Fundamental theorem of calculus by stating that for almost every...

{\displaystyle \mu (A)=\int _{A}f\,d\nu .} Via Lebesgue's decomposition theorem, every σ-finite measure can be decomposed into the sum of an absolutely continuous...

decomposition of σ(T). Let h ∈ H and μh be its corresponding spectral measure on σ(T). According to a refinement of Lebesgue's decomposition theorem,...

integral. It was introduced by Guido Fubini in 1907. The theorem states that if a function is Lebesgue integrable on a rectangle X × Y {\displaystyle X\times...

the Lebesgue measure. The theorem is also sometimes known as the Carathéodory–Fréchet extension theorem, the Carathéodory–Hopf extension theorem, the...

\mu } is not a Dirac delta distribution at zero. By Lebesgue's decomposition theorem, we can decompose μ {\displaystyle \mu } into a sum of a regular measure...

Hobby–Rice theorem (mathematical analysis) Kōmura's theorem (measure theory) Lebesgue's decomposition theorem (measure theory) Lebesgue's density theorem (measure...

processes, the Karhunen–Loève theorem (named after Kari Karhunen and Michel Loève), also known as the Kosambi–Karhunen–Loève theorem states that a stochastic...

. {\displaystyle \mu \perp \nu .} A refined form of Lebesgue's decomposition theorem decomposes a singular measure into a singular continuous measure...

In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D (surface in R...

is a theorem in set-theoretic geometry, which states the following: Given a solid ball in three-dimensional space, there exists a decomposition of the...

The Lebesgue integral describes better how and when it is possible to take limits under the integral sign (via the monotone convergence theorem and dominated...

stochastics. New York: Springer. p. 57. ISBN 9780387878584. see Lebesgue's decomposition theorem Erhan, Çınlar (2011). Probability and stochastics. New York:...

In mathematics, the mean value theorem (or Lagrange's mean value theorem) states, roughly, that for a given planar arc between two endpoints, there is...

functions of real arguments, and used the sine and cosine functions in the decomposition. Many other Fourier-related transforms have since been defined, extending...

{\mathcal {A}},\mu )} . This allows for a refinement of Lebesgue's decomposition theorem, decomposing μ into three mutually singular parts μ = μ a c + μ s...

distributions in two dimensions.[citation needed] Singular measure Lebesgue's decomposition theorem "Singular distribution - Encyclopedia of Mathematics". encyclopediaofmath...

space Lebesgue–Stieltjes integration Lebesgue–Vitali theorem Lebesgue spine Lebesgue's lemma Lebesgue's decomposition theorem Lebesgue's density theorem Lebesgue's...

combination of the Radon-Nikodym and Lebesgue decomposition theorems, any such measure can be uniquely decomposed into d μ = w ( θ ) d θ 2 π + d μ s {\displaystyle...

In multivariable calculus, the implicit function theorem is a tool that allows relations to be converted to functions of several real variables. It does...

of a subset S around which there are no other points of S Lebesgue's decomposition theorem Singleton (mathematics) – Set with exactly one element Singular...

and related branches of mathematics, Lebesgue–Stieltjes integration generalizes both Riemann–Stieltjes and Lebesgue integration, preserving the many advantages...

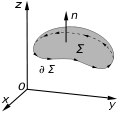
theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls, or simply the curl theorem,...

In calculus, Taylor's theorem gives an approximation of a k {\textstyle k} -times differentiable function around a given point by a polynomial of degree...