mathematics, a logarithm of a matrix is another matrix such that the matrix exponential of the latter matrix equals the original matrix. It is thus a generalization...

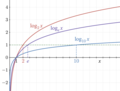
the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of 1000...

square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product BB...

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately...

a disambiguation page; see common logarithm for the traditional concept of mantissa; see significand for the modern concept used in computing. Matrix...

in order to simplify and drastically speed up computation. Tables of logarithms and trigonometric functions were common in math and science textbooks...

In mathematics, a matrix (pl.: matrices) is a rectangular array of numbers or other mathematical objects with elements or entries arranged in rows and...

/2})=2\,{\frac {-i\pi }{2}}=-i\pi } Regardless of which branch of the logarithm is used, a similar failure of the identity will exist. The best that can be...

the mathematical discipline of matrix theory, a Jordan matrix, named after Camille Jordan, is a block diagonal matrix over a ring R (whose identities are...

Matrix exponential Logarithm of a matrix Lie product formula (Trotter product formula) Lie group–Lie algebra correspondence Derivative of the exponential...

\left({\frac {tr(A)}{2}}I-A\right)f'\left({\frac {tr(A)}{2}}\right).} Matrix polynomial Matrix root Matrix logarithm Matrix exponential Matrix sign function...

square root of a matrix, matrix exponential, and logarithm of a matrix are basic examples of hypercomplex analysis. The function theory of diagonalizable...

Both of the above are derived from the following two equations that define a logarithm: (note that in this explanation, the variables of x {\displaystyle...

the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. It is used to solve systems of linear...

mathematics, the determinant of an m-by-m skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries, a polynomial with integer...

unique self-adjoint logarithm of the matrix P {\displaystyle P} . This decomposition is useful in computing the fundamental group of (matrix) Lie groups. The...

Index of a vector field, an integer that helps to describe the behaviour of a vector field around an isolated zero Index, or the discrete logarithm of a number...

determinant is a scalar-valued function of the entries of a square matrix. The determinant of a matrix A is commonly denoted det(A), det A, or |A|. Its value...

{q^{n}}{n!}}=e^{a}\left(\cos \|\mathbf {v} \|+{\frac {\mathbf {v} }{\|\mathbf {v} \|}}\sin \|\mathbf {v} \|\right),} and the logarithm is ln ⁡ ( q ) =...

In quantum mechanics, a density matrix (or density operator) is a matrix used in calculating the probabilities of the outcomes of measurements performed...

is a density matrix, t r {\displaystyle \mathrm {tr} } is a trace operator and ln {\displaystyle \ln } is a matrix logarithm. The density matrix formalism...

matrix addition, matrix multiplication and operations derived from these), functions of matrices (such as matrix exponentiation and matrix logarithm,...

of the matrix-logarithm PL7 and then application of the matrix exponential. The first example below uses the squares of the values of the log-matrix and...

discrete logarithm problem, the quadratic residuosity problem, the RSA inversion problem, and the problem of computing the permanent of a matrix are each...

values in the positive reals. For example, since the logarithm of a product is the sum of the logarithms of the factors, we have ( log ⁡ u v ) ′ = ( log ⁡ u...

objects from a collection. For example, in the adjacent picture, there are 5 − 2 peaches—meaning 5 peaches with 2 taken away, resulting in a total of 3 peaches...

likelihood of θ given X is always proportional to the probability f(X; θ), their logarithms necessarily differ by a constant that is independent of θ, and...

index calculus algorithm is a probabilistic algorithm for computing discrete logarithms. Dedicated to the discrete logarithm in ( Z / q Z ) ∗ {\displaystyle...

satisfy ATJA = J. Thus, the matrix exponential of a Hamiltonian matrix is symplectic. However the logarithm of a symplectic matrix is not necessarily Hamiltonian...

0}\right)} is not a non-positive real number (a positive or a non-real number), the resulting principal value of the complex logarithm is obtained with...