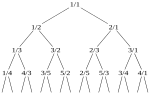
mathematics, Minkowski's question-mark function, denoted ?(x), is a function with unusual fractal properties, defined by Hermann Minkowski in 1904. It...

asterisk. In mathematics, "?" commonly denotes Minkowski's question mark function. In linear logic, the question mark denotes one of the exponential modalities...

fractal curves, including the Cantor function, Cesàro–Faber curve (Lévy C curve), Minkowski's question mark function, blancmange curve, and the Koch curve...

mark (butterfly) or Polygonia interrogationis ? function or Minkowski's question-mark function ?:, in computer programming, a ternary operator Elvis operator...

\mathbb {Z} ).} Note that the Cantor function bears more than a passing resemblance to Minkowski's question-mark function. In particular, it obeys the exact...

theorem Minkowski's question mark function Abraham–Minkowski controversy Hasse–Minkowski theorem Minkowski separation theorem Smith–Minkowski–Siegel mass...

are central to the constructions of the dyadic solenoid, Minkowski's question-mark function, Daubechies wavelets, Thompson's group, Prüfer 2-group, surreal...

singularity Generalized function Distribution Minkowski's question-mark function (**) This condition depends on the references "Singular function", Encyclopedia...

otherwise. Minkowski's question mark function: Derivatives vanish on the rationals. Weierstrass function: is an example of continuous function that is nowhere...

polytopes Minkowski's second theorem Minkowski space Minkowski's bound Minkowski's theorem in geometry of numbers Minkowski–Hlawka theorem Minkowski–Steiner...

describes the self-similarity symmetries of the Cantor function, Minkowski's question mark function, and the Koch snowflake, each being a special case of...

rational numbers. The correspondence is explicitly provided by Minkowski's question mark function, and an explicit construction is given in that article. It...

unbounded linear orders are order-isomorphic. For instance, Minkowski's question-mark function produces an isomorphism (a one-to-one order-preserving correspondence)...

another approach to the problem is to generalise Minkowski's question-mark function. This function ? : [0, 1] → [0, 1] also picks out quadratic irrational...

are provided by Minkowski's question-mark function. If f {\displaystyle f} is an order isomorphism, then so is its inverse function. Also, if f {\displaystyle...

{p}{q}}\right)+{}?\left({\frac {r}{s}}\right)\right)} where ? is Minkowski's question mark function. A positive rational number is one in the form a / b {\displaystyle...

Farey fractions which are seen in the Mandelbrot set with Minkowski's question-mark function and the modular group Gamma. The backwards shift operator...

bodies Minkowski's question mark function Minkowski's second theorem Minkowski's theorem in geometry of numbers Minkowski–Bouligand dimension Minkowski cover...

1]} , but has zero derivative almost everywhere. The Minkowski question-mark function is continuous and strictly increasing but has zero derivative almost...

numbers and continued fractions can also be used to evaluate Minkowski's question mark function; however, in the Calkin–Wilf tree the binary numbers are integers...

Lévy's constant Lochs' theorem Gauss–Kuzmin–Wirsing operator Minkowski's question mark function Generalized continued fraction Kronecker's theorem Thue–Siegel–Roth...

The proofs of these results use the back-and-forth method. Minkowski's question mark function can be used to determine the order isomorphisms between the...

irrationals. The correspondence is explicitly provided by Minkowski's question-mark function. That article also reviews tools that make it easy to work...

number exactly once, but it is not a binary search tree. Minkowski's question-mark function, whose definition for rational arguments is closely related...

0 and that are not eventually constant. Formally, f is the Minkowski question mark function, {0, 1}ω is the Cantor space and ωω is the Baire space.) Observe...

blancmange curve. Cantor function (also known as the Devil's staircase) Minkowski's question mark function Weierstrass function Dyadic transformation Weisstein...

tangent line to any point is impossible. Unlike the earlier Weierstrass function where the proof was purely analytical, the Koch snowflake was created to...

particular function of matrices with real, nonnegative entries satisfying a summation condition Problems in Latin squares – open questions concerning...

prevent an event horizon from existing, depending on the acceleration function chosen. The observer never touches the horizon and never passes a location...

Hawking (after physicist Stephen Hawking), George Minkowski (after mathematician Hermann Minkowski), Richard Alpert (the birth name of spiritual teacher...