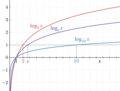
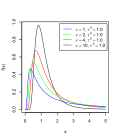
probability theory and statistics, the Exponential-Logarithmic (EL) distribution is a family of lifetime distributions with decreasing failure rate, defined...

in a process with no memory. The exponential-logarithmic distribution The F-distribution, which is the distribution of the ratio of two (normalized)...

over the mean, and a vague prior probability (such as an exponential or gamma distribution) over the positive reals for the sample size, if they are...

normal distribution. Equivalently, if Y has a normal distribution, then the exponential function of Y, X = exp(Y), has a log-normal distribution. A random...

It is the discrete version of the same property found in the exponential distribution.: 228  The property asserts that the number of previously failed...

gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and...

In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formula f ′ f {\displaystyle...

identified using bundle plots. In general, power-law distributions are plotted on doubly logarithmic axes, which emphasizes the upper tail region. The most...

8, 16, and 32 (i.e., 21, 22, 23, 24, 25). Exponential growth curves are often depicted on a logarithmic scale graph. The markings on slide rules are...

cumulative distribution function of an exponential distribution with rate α. Pareto distribution can be constructed by hierarchical exponential distributions. Let...

them to the exponential function in the 18th century, and who also introduced the letter e as the base of natural logarithms. Logarithmic scales reduce...

chi-squared distribution simplifies to an exponential distribution with mean equal to two (rate equal to half). The complementary cumulative distribution function...

differentiation Logarithmic distribution Logarithmic form Logarithmic graph paper Logarithmic growth Logarithmic identities Logarithmic number system Logarithmic scale...

underlying distribution is normal. Unlike more widely known distributions such as the normal distribution and the exponential distribution, the chi-squared...

heavy-tailed distributions are probability distributions whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution...

about properties of the Dirichlet distribution. Because the Dirichlet distribution is an exponential family distribution it has a conjugate prior. The conjugate...

analysis Exponential dispersion model Exponential distribution Exponential family Exponential-logarithmic distribution Exponential power distribution – redirects...

and geometric growth (whose curve he calls a logarithmic curve, instead of the modern term exponential curve), and thus "logistic growth" is presumably...

the maximum entropy distribution for a fixed first inverse moment ( E ( 1 / X ) ) {\displaystyle (E(1/X))} and first logarithmic moment ( E ( ln ⁡ ( X...

_{0}^{\infty }d\tau \,t^{n}\,\rho (\tau ).} The first logarithmic moment of the distribution of simple-exponential relaxation times is ⟨ ln ⁡ τ ⟩ = ( 1 − 1 β )...

identically distributed random variables, each one having the logarithmic series distribution Log(p), with probability mass function f ( k ; r , p ) = −...

in R). Exponential distribution Exponential-logarithmic distribution Gamma distribution Generalized gamma distribution Hypertabastic distribution Lindley...

\ln(b)).} This relationship is true regardless of the base of the logarithmic or exponential function. If log a ⁡ ( Y ) {\displaystyle \log _{a}(Y)} is uniform...

mathematics, an exponential sum may be a finite Fourier series (i.e. a trigonometric polynomial), or other finite sum formed using the exponential function,...

can also measure the reflectivity of cloud drops and ice. For an exponential distribution of reflectors, Z is expressed by: Z = ∫ 0 D m a x N 0 e − Λ D D...

quadratic and the Cauchy tails are logarithmic. B σ ( α , β ) {\displaystyle B_{\sigma }(\alpha ,\beta )} forms an exponential family with natural parameters...

(1-(\omega \tau )^{2\alpha })^{\beta }}} The first logarithmic moment of this distribution, the average logarithmic relaxation time is ⟨ ln ⁡ τ D ⟩ = ln ⁡ τ +...

In mathematics, many logarithmic identities exist. The following is a compilation of the notable of these, many of which are used for computational purposes...

Poisson distribution where mean and variance are the same. In practice, almost only densities of gamma distributions, logarithmic normal distributions and...

is assumed to be equally likely): The Taylor series expansion of the exponential function (the constant e ≈ 2.718281828) e x = 1 + x + x 2 2 ! + ⋯ {\displaystyle...