mathematics, the gamma function (represented by Γ, capital Greek letter gamma) is the most common extension of the factorial function to complex numbers...

In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems...

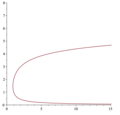
mathematics, the inverse gamma function Γ − 1 ( x ) {\displaystyle \Gamma ^{-1}(x)} is the inverse function of the gamma function. In other words, y = Γ...

{\displaystyle \Gamma } is used as a symbol for: In mathematics, the gamma function (usually written as Γ {\displaystyle \Gamma } -function) is an extension...

reciprocal gamma function is the function f ( z ) = 1 Γ ( z ) , {\displaystyle f(z)={\frac {1}{\Gamma (z)}},} where Γ(z) denotes the gamma function. Since...

The gamma function is an important special function in mathematics. Its particular values can be expressed in closed form for integer, half-integer, and...

gamma function Γp is a generalization of the gamma function. It is useful in multivariate statistics, appearing in the probability density function of...

scaled inverse chi-squared distribution. The inverse gamma distribution's probability density function is defined over the support x > 0 {\displaystyle x>0}...

the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial...

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function: ψ ( z ) = d d z ln ⁡ Γ ( z ) = Γ ′ ( z ) Γ ( z )...

Hadamard's gamma function, named after Jacques Hadamard, is an extension of the factorial function, different from the classical gamma function (it is an...

for the gamma function and the Barnes G-function. The asymptotic expansion of the gamma function, Γ ( 1 / x ) ∼ x − γ {\displaystyle \Gamma (1/x)\sim...

distribution functions of the gamma distribution vary based on the chosen parameterization, both offering insights into the behavior of gamma-distributed...

gamma function Γ N {\displaystyle \Gamma _{N}} is a generalization of the Euler gamma function and the Barnes G-function. The double gamma function was...

Gamma correction or gamma is a nonlinear operation used to encode and decode luminance or tristimulus values in video or still image systems. Gamma correction...

factorial function to a continuous function of complex numbers, except at the negative integers, the (offset) gamma function. Many other notable functions and...

Many values of the theta function and especially of the shown phi function can be represented in terms of the gamma function: φ ( exp ⁡ ( − 2 π ) ) =...

z ) {\displaystyle \Gamma (z+1)=z\Gamma (z)} . The Hankel contour can be used to help derive an expression for the Gamma function, based on the fundamental...

function, Polygamma function Incomplete beta function Incomplete gamma function K-function Multivariate gamma function: A generalization of the Gamma...

{d} x} is the gamma function. The Riemann zeta function is defined for other complex values via analytic continuation of the function defined for σ >...

the elliptic gamma function is a generalization of the q-gamma function, which is itself the q-analog of the ordinary gamma function. It is closely...

\mathbb {C} } defined as the (m + 1)th derivative of the logarithm of the gamma function: ψ ( m ) ( z ) := d m d z m ψ ( z ) = d m + 1 d z m + 1 ln ⁡ Γ ( z )...

In mathematics, the p-adic gamma function Γp is a function of a p-adic variable analogous to the gamma function. It was first explicitly defined by Morita...

_{k=0}^{\infty }{\frac {z^{k}}{\Gamma (\alpha k+1)}},} where Γ ( x ) {\displaystyle \Gamma (x)} is the gamma function, and α {\displaystyle \alpha } is...

the functional equation for the Gamma function, Γ ( s ) Γ ( 1 − s ) = π sin ⁡ ( π s ) , {\displaystyle \Gamma (s)\Gamma (1-s)={\pi \over \sin(\pi s)},}...

G-function G(z) is a function that is an extension of superfactorials to the complex numbers. It is related to the gamma function, the K-function and...

{\displaystyle q} -gamma function, or basic gamma function, is a generalization of the ordinary gamma function closely related to the double gamma function. It was...

\Gamma (n)=(n-1)!} . When the gamma function is evaluated at half-integers, the result contains π. For example, Γ ( 1 2 ) = π {\displaystyle \Gamma {\bigl...

distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution f ( x ; x 0 , γ ) {\displaystyle f(x;x_{0},\gamma )} is the distribution...

{1}{n}}\right)\right).} An alternative formula for n ! {\displaystyle n!} using the gamma function is n ! = ∫ 0 ∞ x n e − x d x . {\displaystyle n!=\int _{0}^{\infty }x^{n}e^{-x}\...