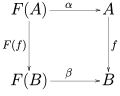
In mathematics, an initial algebra is an initial object in the category of F-algebras for a given endofunctor F. This initiality provides a general framework...

programming, such as lists and trees. The main related concepts are initial F-algebras which may serve to encapsulate the induction principle, and the dual...

homomorphism from an initial algebra into some other algebra. Catamorphisms provide generalizations of folds of lists to arbitrary algebraic data types, which...

and anarchic algebra. From a category theory perspective, a term algebra is the initial object for the category of all X-generated algebras of the same...

In computer science, algebraic semantics is a formal approach to programming language theory that uses algebraic methods for defining, specifying, and...

being the theory having an empty set of sentences (in analogy to an initial algebra). Theories with a non-empty set of equations are known as equational...

In category theory, a branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely...

an algebraic data type (ADT) is a kind of composite data type, i.e., a data type formed by combining other types. Two common classes of algebraic types...

mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables...

In mathematics, a Lie algebra (pronounced /liː/ LEE) is a vector space g {\displaystyle {\mathfrak {g}}} together with an operation called the Lie bracket...

Algebraic notation is the standard method of chess notation, used for recording and describing moves. It is based on a system of coordinates to identify...

mathematics, and more specifically in abstract algebra, a *-algebra (or involutive algebra; read as "star-algebra") is a mathematical structure consisting of...

James W.; Wagner, Eric G.; Wright, Jesse B. (1977). "Initial algebra semantics and continuous algebras". Journal of the ACM. 24 (1): 68–95. doi:10.1145/321992...

In algebra, the zero object of a given algebraic structure is, in the sense explained below, the simplest object of such structure. As a set it is a singleton...

In mathematics, an associative algebra A over a commutative ring (often a field) K is a ring A together with a ring homomorphism from K into the center...

Semantics (computer science) Semantics of logic Garden-path sentence Initial algebra Levels of Processing model Opaque context — another problem for compositionality...

Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems...

mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure...

language, then final types coincide with initial types, and the corresponding final coalgebra and initial algebra form an isomorphism. Corecursion is then...

Synthese 19 (3/4): 325–373 (1969). Goguen, J.A. and J.W. Thatcher. "Initial algebra semantics", in Proceedings, Fifteenth Symposium on Switching and Automata...

In mathematics, a ring is an algebraic structure consisting of a set with two binary operations called addition and multiplication, which obey the same...

modal logic.[citation needed] Initial algebra Coinduction Coalgebra B. Jacobs and J. Rutten, A Tutorial on (Co)Algebras and (Co)Induction. EATCS Bulletin...

labeled by a has B(a)-many subtrees. Each W-type is isomorphic to the initial algebra of a so-called polynomial functor. Let 0, 1, 2, etc. be finite types...

sometimes referred to as lenses. Morphism Morphisms of F-algebras From an initial algebra to an algebra: Catamorphism An anamorphism followed by an catamorphism:...

monoid (= commutative ring) R on an object (= ring) A of Ring is an R-algebra. The category of rings has a number of important subcategories. These include...

summation of these leaf nodes. Morphism Morphisms of F-algebras From an initial algebra to an algebra: Catamorphism From a coalgebra to a final coalgebra:...

central notions of commutative algebra and homological algebra, and are used widely in algebraic geometry and algebraic topology. In a vector space, the...

geometric algebra (also known as a Clifford algebra) is an algebra that can represent and manipulate geometrical objects such as vectors. Geometric algebra is...

In algebra, the kernel of a homomorphism (function that preserves the structure) is generally the inverse image of 0 (except for groups whose operation...

Commutative algebra, first known as ideal theory, is the branch of algebra that studies commutative rings, their ideals, and modules over such rings. Both...