The Lehmer random number generator (named after D. H. Lehmer), sometimes also referred to as the Park–Miller random number generator (after Stephen K. Park...
28 KB (3,636 words) - 13:41, 3 December 2024
1949, he presented the pseudorandom number generator now known as the Lehmer random number generator. D. H. Lehmer wrote the article "The Machine Tools...
13 KB (1,371 words) - 15:36, 3 December 2024
constants that specify the generator. If c = 0, the generator is often called a multiplicative congruential generator (MCG), or Lehmer RNG. If c ≠ 0, the method...
43 KB (4,861 words) - 15:40, 14 March 2025
Random number generators are important in many kinds of technical applications, including physics, engineering or mathematical computer studies (e.g.,...
23 KB (1,461 words) - 23:11, 6 March 2025
pseudorandom number generators, the resulting sequences are functions of the supplied seed values. An MWC generator is a special form of Lehmer random number generator...
36 KB (4,065 words) - 23:24, 5 May 2025
after Derrick Henry Lehmer Lehmer random number generator, named after D. H. Lehmer Lehmer sieve Lucas–Lehmer test Lucas–Lehmer–Riesel test, in mathematics...
2 KB (233 words) - 19:39, 10 April 2018
16,807 (redirect from 16807 (number))
with seven labeled nodes. Several authors have suggested a Lehmer random number generator: X k + 1 = 16807 ⋅ X k mod 2147483647 {\displaystyle...
2 KB (193 words) - 13:23, 30 March 2025
quasi-Monte Carlo methods use quasi-random number generators. Random selection, when narrowly associated with a simple random sample, is a method of selecting...
34 KB (4,316 words) - 10:18, 11 February 2025
A permuted congruential generator (PCG) is a pseudorandom number generation algorithm developed in 2014 by Dr. M.E. O'Neill which applies an output permutation...
13 KB (1,678 words) - 14:24, 15 March 2025
Marsaglia's theorem (category Random number generation)
the modulus and multiplier in a Lehmer random number generator will lead to a short period for the sequence of random numbers. Marsaglia's result may...
4 KB (533 words) - 02:56, 16 February 2025
the words "let X1,...,Xn be independent random variables...". Yet as D. H. Lehmer stated in 1951: "A random sequence is a vague notion... in which each...
9 KB (1,191 words) - 00:02, 21 August 2024
secure pseudo-random number generator Middle-square method Blum Blum Shub ACORN ISAAC Lagged Fibonacci generator Linear congruential generator Mersenne twister...
10 KB (938 words) - 19:59, 21 December 2024
65,537 (redirect from 65537 (number))
proper padding). 65537 is also used as the modulus in some Lehmer random number generators, such as the one used by ZX Spectrum, which ensures that any...
4 KB (539 words) - 00:17, 31 October 2024
"Mersenne Twister: A 623-dimensionally equidistributed uniform pseudo-random number generator". ACM Transactions on Modeling and Computer Simulation. 8 (1):...
117 KB (14,179 words) - 16:20, 4 May 2025
Probability distribution (redirect from Continuous Random Variable)
pseudorandom number generator that produces numbers X {\displaystyle X} that are uniformly distributed in the half-open interval [0, 1). These random variates...
48 KB (6,688 words) - 17:43, 6 May 2025
which enhance randomness beyond what manual shuffling can achieve. With the rise of online casinos, digital random number generators (RNGs) have become...
23 KB (2,626 words) - 17:21, 17 April 2025
Variance (redirect from Random variance)
stable alternatives, see algorithms for calculating variance. If the generator of random variable X {\displaystyle X} is discrete with probability mass function...
61 KB (10,215 words) - 11:05, 7 May 2025
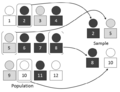
Sampling (statistics) (redirect from Random sampling)
correct for non-response. Random number table Mathematical algorithms for pseudo-random number generators Physical randomization devices such as coins, playing...
55 KB (7,545 words) - 05:53, 9 May 2025
Mersenne prime (redirect from Mersenne number)
simple efficient test to determine whether a given Mersenne number is prime: the Lucas–Lehmer primality test (LLT), which makes it much easier to test the...
71 KB (6,408 words) - 15:57, 8 May 2025
Pi (redirect from Ludolph transcendental number)
\end{aligned}}} This probability can be used in conjunction with a random number generator to approximate π using a Monte Carlo approach. The solution to...
147 KB (17,250 words) - 19:04, 26 April 2025
Random compact set Random element Random function Random measure Random number generator Random variate Random vector Randomness Stochastic process Relationships...
42 KB (6,634 words) - 09:46, 2 May 2025
versus a control group) using randomization, such as by a chance procedure (e.g., flipping a coin) or a random number generator. This ensures that each participant...
12 KB (1,361 words) - 16:38, 4 May 2025
Monte Carlo method (category Randomized algorithms)
computational cost, the curse of dimensionality, the reliability of random number generators, and the verification and validation of the results. Monte Carlo...
91 KB (10,690 words) - 23:18, 29 April 2025
Central limit theorem (category Wikipedia articles needing page number citations from July 2023)
an integer number n {\displaystyle n} of random variables and taking n → ∞ {\displaystyle n\to \infty } , the sum can be of a random number N {\displaystyle...
67 KB (9,171 words) - 16:52, 28 April 2025
Discrete logarithm (redirect from Index (number theory))
a cyclic group G {\displaystyle G} under multiplication, and 10 is a generator for this group. The discrete logarithm log 10 a {\displaystyle \log...
17 KB (2,506 words) - 02:19, 27 April 2025
whether a given number is prime. Prime numbers are also used in computing for checksums, hash tables, and pseudorandom number generators. In 1974, Donald...
94 KB (12,031 words) - 18:57, 12 May 2025
Coprime integers (redirect from Relatively prime number)
algorithm and its faster variants such as binary GCD algorithm or Lehmer's GCD algorithm. The number of integers coprime with a positive integer n, between 1 and...
16 KB (2,409 words) - 15:43, 27 April 2025
{O}}\left(b^{-1}\right)} Hence we can expect the generator to run no more Miller–Rabin tests than a number proportional to b. Taking into account the worst-case...
38 KB (5,639 words) - 20:26, 3 May 2025
mathematics, the Pocklington–Lehmer primality test is a primality test devised by Henry Cabourn Pocklington and Derrick Henry Lehmer. The test uses a partial...
15 KB (1,909 words) - 20:05, 9 February 2025
Euler's totient function (redirect from Totient number)
computed without factoring n. If p is prime, then φ(p) = p − 1. In 1932 D. H. Lehmer asked if there are any composite numbers n such that φ(n) divides n − 1...
44 KB (6,524 words) - 05:30, 5 May 2025