field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann...

In geometry, the Möbius–Kantor configuration is a configuration consisting of eight points and eight lines, with three points on each line and three lines...

Heawood graph is the Levi graph of the Fano plane. It is also known as the (3,6)-cage, and is 3-regular with 14 vertices. The Möbius–Kantor graph is the...

Leipzig. Möbius died in Leipzig in 1868 at the age of 77. His son Theodor was a noted philologist. He is best known for his discovery of the Möbius strip...

the Möbius–Kantor graph G(8, 3), the dodecahedral graph G(10, 2) and the Nauru graph G(12, 5). The characteristic polynomial of the Desargues graph is...

Look up Möbius in Wiktionary, the free dictionary. Moebius, Mœbius, Möbius or Mobius may refer to: August Ferdinand Möbius (1790–1868), German mathematician...

individual graphs are cubic and symmetric, including the utility graph, the Petersen graph, the Heawood graph, the Möbius–Kantor graph, the Pappus graph, the...

Petersen graphs also include the n-prism G ( n , 1 ) {\displaystyle G(n,1)} the Dürer graph G ( 6 , 2 ) {\displaystyle G(6,2)} , the Möbius-Kantor graph G (...

the Möbius–Kantor graph, for example, has crossing number 4 and is toroidal. Any toroidal graph has chromatic number at most 7. The complete graph K7 provides...

graphs are the n {\displaystyle n} -prism G ( n , 1 ) {\displaystyle G(n,1)} , the Dürer graph G ( 6 , 2 ) {\displaystyle G(6,2)} , the Möbius-Kantor...

In geometry, the Möbius–Kantor polygon is a regular complex polygon 3{3}3, , in C 2 {\displaystyle \mathbb {C} ^{2}} . 3{3}3 has 8 vertices, and 8 edges...

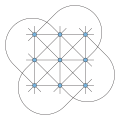
spindle and Golomb graph (small 4-chromatic unit distance graphs). All generalized Petersen graphs, such as the Möbius–Kantor graph depicted, are non-strict...

In the mathematical field of graph theory, a graph G is symmetric or arc-transitive if, given any two ordered pairs of adjacent vertices ( u 1 , v 1 )...

3-regular graphs. Every strongly regular graph is symmetric, but not vice versa. Heawood graph Möbius–Kantor graph Pappus graph Desargues graph Nauru graph Coxeter...

the Petersen graph G ( 5 , 2 ) {\displaystyle G(5,2)} , the Möbius–Kantor graph G ( 8 , 3 ) {\displaystyle G(8,3)} , the dodecahedral graph G ( 10 , 2 )...

Möbius–Kantor configuration is the unique (83). Each incidence structure C corresponds to a bipartite graph called the Levi graph or incidence graph of...

Austro-Hungarian Empire. He is known for the Möbius–Kantor configuration and the Möbius-Kantor graph. Kantor studied mathematics and physics at the Technische...

smallest 4-crossing cubic graph is the Möbius-Kantor graph, with 16 vertices. The smallest 5-crossing cubic graph is the Pappus graph, with 18 vertices. The...

The Möbius–Kantor graph, the Cayley graph of the Pauli group with generators X, Y, and Z...

In geometry, the Möbius configuration or Möbius tetrads is a certain configuration in Euclidean space or projective space, consisting of two tetrahedra...

various individual (finite) graphs. The columns 'vertices', 'edges', 'radius', 'diameter', 'girth', 'P' (whether the graph is planar), χ (chromatic number)...

graph formed by connecting an outer polygon and an inner star with the same number of points; for instance, this applies to the Möbius–Kantor graph and...

1934 Seifert, Threlfall: Variationsrechnung im Großen, Teubner 1938 Möbius–Kantor graph Schwarz triangle tessellation Gabriele Dörflinger: William R. M....

configuration, (123 94), points indexed 1...12 can have configuration table: Möbius–Kantor configuration Removing any one point and its four incident lines from...

In the mathematical field of graph theory, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by H. S. M. Coxeter and Robert...

abstractly-described system of points and lines has a planar realization; the Möbius–Kantor configuration of eight points and eight lines does not. It is known...

through that point (but not the other points on them) produces the (83) Möbius–Kantor configuration. Given an integer α ≥ 1, a tactical configuration satisfying:...

geometry, but cannot be constructed in the Euclidean plane. (83), the Möbius–Kantor configuration. This configuration describes two quadrilaterals that...

of the graph. Finite Groups of Automorphisms, Cambridge University Press (1971) Algebraic Graph Theory, Cambridge University Press (1974) Graph Theory...

Surveys the major and minor vector systems of the 19th century (Hamilton, Möbius, Bellavitis, Clifford, Grassmann, Tait, Peirce, Maxwell, Macfarlane, MacAuley...