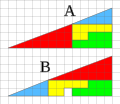
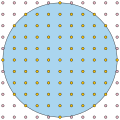
In geometry, Pick's theorem provides a formula for the area of a simple polygon with integer vertex coordinates, in terms of the number of integer points...

Schleisinger and Adolf Josef Pick and died at Theresienstadt concentration camp. Today he is best known for Pick's theorem for determining the area of...

desired. A variant of the Schwarz lemma, known as the Schwarz–Pick theorem (after Georg Pick), characterizes the analytic automorphisms of the unit disc...

Schwarz–Ahlfors–Pick theorem is an extension of the Schwarz lemma for hyperbolic geometry, such as the Poincaré half-plane model. The Schwarz–Pick lemma states...

lattice is coarsely equivalent to Euclidean space. Pick's theorem, first described by Georg Alexander Pick in 1899, provides a formula for the area of a simple...

side lengths (Heron's formula), vectors, coordinates, line integrals, Pick's theorem, or other properties. Heron of Alexandria found what is known as Heron's...

by Alicia K. Harris Pick operating system, a computer operating system Pick's disease, a neurodegenerative disease Pick's theorem in geometry Sertoli...

has motivated various attempts to generalise Nevanlinna and Pick's result. The Nevanlinna–Pick problem can be generalised to that of finding a holomorphic...

in 1957 used them to show that higher-dimensional generalizations of Pick's theorem do not exist. Despite this negative result, Reeve developed an alternative...

Ehrhart polynomials can be seen as a higher-dimensional generalization of Pick's theorem in the Euclidean plane. These polynomials are named after Eugène Ehrhart...

conjectured to be PPP complete. Danzer set Pick's theorem Dirichlet's unit theorem Minkowski's second theorem Ehrhart's volume conjecture Olds, C. D.; Lax...

Minkowski's second theorem (geometry of numbers) Minkowski–Hlawka theorem (geometry of numbers) Monsky's theorem (discrete geometry) Pick's theorem (geometry)...

red dots in the above image) with an area of exactly one grid square (Pick's theorem gives 0 + ⁠4/2⁠ − 1 = 1), which corresponds to the "missing" area. According...

digital images). Study of properties of digital sets; see, for example, Pick's theorem, digital convexity, digital straightness, or digital planarity. Transforming...

angle Holditch's theorem Interactive geometry software Involutes Goat grazing problem Parallel postulate Polygon Star polygon Pick's theorem Shape dissection...

polygon and b is the number of boundary points. This result is known as Pick's theorem. The area between a positive-valued curve and the horizontal axis, measured...

the origin in the square of side 2n, centered at the origin. Using Pick's theorem, the area of the sunburst is 4(|Fn| − 1), where |Fn| is the number of...

geometry: Polyhedral combinatorics Lattice polytopes Ehrhart polynomials Pick's theorem Hirsch conjecture Opaque set Packings, coverings, and tilings are all...

polygon. These include the shoelace formula for arbitrary polygons, and Pick's theorem for polygons with integer vertex coordinates. The convex hull of a simple...

_{F}v_{1}\wedge v_{2}\wedge v_{3}\right\|} Planimeter Polygon area Pick's theorem Heron's formula Mathologer video about Gauss's shoelace formula Bart...

fairy chess piece the wazir form a square lattice graph. Lattice path Pick's theorem Integer triangles in a 2D lattice Regular graph Weisstein, Eric W. "Lattice...

measurement with random placements. According to Pick's theorem, published by Georg Alexander Pick in 1899, the version of the dot planimeter with boundary...

an equally spaced grid such that all its vertices are grid points, Pick's theorem gives a simple formula for the polygon's area based on the numbers of...

numbers Minkowski's theorem Pick's theorem Mahler's compactness theorem Mahler measure Effective results in number theory Mahler's theorem Brun sieve Function...

the area of a shape by counting the lattice points that it contains Pick's theorem, a more precise relationship between area and lattice points covered...

Ren, Ding; Reay, John R. (1987). "The boundary characteristic and Pick's theorem in the Archimedean planar tilings". J. Comb. Theory A. 44 (1): 110–119...

Poincaré–Hopf theorem (also known as the Poincaré–Hopf index formula, Poincaré–Hopf index theorem, or Hopf index theorem) is an important theorem that is used...

In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem relating the flux of a vector field through...

relation bc − ad = 1 holds. This fact may be deduced e.g. with the help of Pick's theorem which expresses the area of a plane triangle whose vertices have integer...

not separated by any point of a lattice and the slope of the lines, Pick's theorem relating the area of a lattice polygon to the number of lattice points...