Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing...

such as polyhedral combinatorics (the study of faces of convex polyhedra), convex geometry (the study of convex sets, in particular combinatorics of their...

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic)...

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices...

stellation and may also be applied to higher-dimensional polytopes. In polyhedral combinatorics and in the general theory of polytopes, a face that has dimension...

Geometric combinatorics is a branch of mathematics in general and combinatorics in particular. It includes a number of subareas such as polyhedral combinatorics...

Lectures in Geometric Combinatorics is a textbook on polyhedral combinatorics. It was written by Rekha R. Thomas, based on a course given by Thomas at...

combinatorial problems are central to combinatorial optimization and polyhedral combinatorics. In economics, convex hulls can be used to apply methods of convexity...

member of the Dutch Society of Science. Since 1994, the Institute of Combinatorics and its Applications has handed out an annual Kirkman medal, named after...

algorithm design manual, p 506, and Computational discrete mathematics: combinatorics and graph theory with Mathematica, p. 290-291 Diestel (2016), p.84 Diestel...

fundamental contributions to the fields of combinatorial optimization, polyhedral combinatorics, discrete mathematics and the theory of computing. He was the recipient...

Motzkin, Victor Klee, and others. They play an important role in polyhedral combinatorics: according to the upper bound theorem, proved by Peter McMullen...

some of the aspects of polytopes studied in discrete geometry: Polyhedral combinatorics Lattice polytopes Ehrhart polynomials Pick's theorem Hirsch conjecture...

Combinatorial commutative algebra Polyhedral combinatorics Algebraic Combinatorics (journal) Journal of Algebraic Combinatorics International Conference on...

of) simplicial polytopes this coincides with the meaning from polyhedral combinatorics. Sometimes the term face is used to refer to a simplex of a complex...

of a convex polytope P is a polyhedral fan that is dual to P. Normal fans have applications to polyhedral combinatorics, linear programming, tropical...

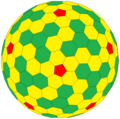
In mathematics, and more specifically in polyhedral combinatorics, a Goldberg polyhedron is a convex polyhedron made from hexagons and pentagons. They...

In geometry, the Perles configuration is a system of nine points and nine lines in the Euclidean plane for which every combinatorially equivalent realization...

In mathematics, and more particularly in polyhedral combinatorics, Eberhard's theorem partially characterizes the multisets of polygons that can form the...

integration. Geometric combinatorics a branch of combinatorics. It includes a number of subareas such as polyhedral combinatorics (the study of faces of...

(0-faces), and the empty set. In some areas of mathematics, such as polyhedral combinatorics, a polytope is by definition convex. In this setting, there is...

solid figure or to its boundary surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term...

dimension and number of vertices. It is one of the central results of polyhedral combinatorics. Originally known as the upper bound conjecture, this statement...

In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope P is another polyhedron or polytope PK formed...

In polyhedral combinatorics, a branch of mathematics, Balinski's theorem is a statement about the graph-theoretic structure of three-dimensional convex...

In the mathematical discipline of polyhedral combinatorics, the Gale transform turns the vertices of any convex polytope into a set of vectors or points...

of combinatorial optimization problems, under the framework of polyhedral combinatorics. The related branch and cut method combines the cutting plane and...

In mathematics, a unique sink orientation is an orientation of the edges of a polytope such that, in every face of the polytope (including the whole polytope...

polytope theory, Kalai's 3d conjecture is a conjecture on the polyhedral combinatorics of centrally symmetric polytopes, made by Gil Kalai in 1989. It...

(729 vertices). In enumerative combinatorics, there are 3n signed subsets of a set of n elements. In polyhedral combinatorics, the hypercube and all other...