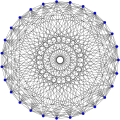
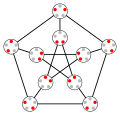
In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed (with...

Richard Rado FRS (28 April 1906 – 23 December 1989) was a German-born British mathematician whose research concerned combinatorics and graph theory. He...

constructed by Richard Rado and is now called the Rado graph or random graph. More recent work has focused on universal graphs for a graph family F: that is...

The Rado graph is an infinite self-complementary graph. An n-vertex self-complementary graph has exactly half as many edges of the complete graph, i.e...

only a single graph with this property, namely the Rado graph. Thus any countably infinite random graph is almost surely the Rado graph, which for this...

countably infinite random graphs in the Erdős–Rényi model are, with probability 1, isomorphic to the highly symmetric Rado graph. The smallest asymmetric...

Erdős–Ko–Rado theorem is that these graphs have fractional chromatic number exactly n / r {\displaystyle n/r} . Paul Erdős, Chao Ko, and Richard Rado proved...

hereditarily finite sets, and defining the adjacency relation of the Rado graph. In computer science, it is used for efficient representations of set...

Coxeter graph Tutte–Coxeter graph Dyck graph Klein graph Foster graph Biggs–Smith graph The Rado graph Folkman graph Gray graph Ljubljana graph Tutte 12-cage...

this graph corresponds in a certain sense to the limit object of G n {\displaystyle G_{n}} as n → + ∞ {\displaystyle n\to +\infty } . Rado graph – Infinite...

tilings by regular polygons infinite Cayley graphs the Rado graph Two countable vertex-transitive graphs are called quasi-isometric if the ratio of their...

logic of graphs. Moreover, the limiting probability is one if and only if the infinite Rado graph has the property. For instance, a random graph in this...

proofs of the Erdős–Ko–Rado theorem and its analogue for intersecting families of subspaces over finite fields. For general graphs which are not necessarily...

infinite), their complement graphs, the Henson graphs together with their complement graphs, and the Rado graph. If a graph is 5-ultrahomogeneous, then...

Many other symmetric graphs can be classified as circulant graphs (but not all). The Rado graph forms an example of a symmetric graph with infinitely many...

earlier neighbors. (Only the Rado graph has such a sequence.) He then defines Gi to be the induced subgraph of the Rado graph formed by removing the final...

structure. In graph theory, the graph whose vertices correspond to hereditarily finite sets and edges correspond to set membership is the Rado graph or random...

there is a specific infinite graph, the Rado graph R {\displaystyle R} , such that the sentences modeled by the Rado graph are exactly the ones for which...

Turán graphs, 3 × 3 rook's graphs, and the 5-cycle. The infinite Rado graph is countably ultrahomogeneous. There are only two connected graphs that are...

Erdős–Rényi model of random graphs, when applied to countably infinite graphs, almost surely produces a unique graph, the Rado graph. any two many-complete...

\lambda _{0}} has multiplicity 1. The Erdős–Ko–Rado theorem states that the independence number of the Kneser graph K(n, k) for n ≥ 2 k {\displaystyle n\geq...

Erdős–Ko–Rado theorem (which can be formulated in terms of independent sets in Kneser graphs), these are the unique maximum independent sets in this graph. It...

language of graphs.) The theory of random graphs is ω categorical, complete, and decidable, and its countable model is called the Rado graph. A statement...

combinatorics, algebraic, differential, discrete and Euclidean geometries, graph theory, group theory, model theory, number theory, set theory, Ramsey theory...

mathematics, Johnson graphs are a special class of undirected graphs defined from systems of sets. The vertices of the Johnson graph J ( n , k ) {\displaystyle...

Rado's theorem is a theorem from the branch of mathematics known as Ramsey theory. It is named for the German mathematician Richard Rado. It was proved...

particular any unclassifiable or deep theory, such as the theory of the Rado graph. ℶ d + 1 ( | α + ω | ) {\displaystyle \beth _{d+1}(|\alpha +\omega |)}...

hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two...

orders without endpoints (Cantor's isomorphism theorem) The theory of the Rado graph The theory of infinite linear spaces over any finite field The theory...

G p h {\displaystyle \mathbf {Gph} } of all finite graphs, whose Fraïssé limit is the Rado graph. For any prime p, the Fraïssé limit of the class of...