In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces...

particularly q-analog theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties...

Maass form, and a mock theta function is essentially a mock modular form of weight ⁠1/2⁠. The first examples of mock theta functions were described by Srinivasa...

Riemann–Siegel theta function is defined in terms of the gamma function as θ ( t ) = arg ⁡ ( Γ ( 1 4 + i t 2 ) ) − log ⁡ π 2 t {\displaystyle \theta (t)=\arg...

functions. Elliptic curve Schwarz–Christoffel mapping Carlson symmetric form Jacobi theta function Ramanujan theta function Dixon elliptic functions Abel...

Theta (UK: /ˈθiːtə/ , US: /ˈθeɪtə/) uppercase Θ or ϴ; lowercase θ or ϑ; Ancient Greek: θῆτα thē̂ta [tʰɛ̂ːta]; Modern: θήτα thī́ta [ˈθita]) is the eighth...

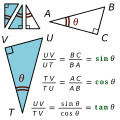
trigonometric function alternatively written arcsin ⁡ x . {\displaystyle \arcsin x\,.} The equation θ = sin − 1 ⁡ x {\displaystyle \theta =\sin ^{-1}x}...

+2b\cdot \cos \theta \sin \theta +c\cdot \sin ^{2}\theta )}},\\\sigma _{Y}^{2}&={\frac {1}{2(a\cdot \sin ^{2}\theta -2b\cdot \cos \theta \sin \theta +c\cdot...

variables. Theta function may also refer to: q-theta function, θ ( z ; q ) {\displaystyle \theta (z;q)} , a type of q-series Theta function of a lattice...

trigonometric functions. For example, if x = sin ⁡ θ {\displaystyle x=\sin \theta } , then d x / d θ = cos ⁡ θ = 1 − x 2 , {\textstyle dx/d\theta =\cos \theta ={\sqrt...

In mathematics, the q-theta function (or modified Jacobi theta function) is a type of q-series which is used to define elliptic hypergeometric series...

In mathematics, the Neville theta functions, named after Eric Harold Neville, are defined as follows: θ c ( z , m ) = 2 π q ( m ) 1 / 4 m 1 / 4 K ( m...

via Bayes' rule. The likelihood function, parameterized by a (possibly multivariate) parameter θ {\textstyle \theta } , is usually defined differently...

\,\tau >0.} The theta function of a lattice is then a holomorphic function on the upper half-plane. Furthermore, the theta function of an even unimodular...

{\displaystyle \theta } , the sine and cosine functions are denoted as sin ⁡ ( θ ) {\displaystyle \sin(\theta )} and cos ⁡ ( θ ) {\displaystyle \cos(\theta )} ....

the remaining factor can be regarded as a function of the spherical angular coordinates θ {\displaystyle \theta } and φ {\displaystyle \varphi } only, or...

In mathematics, the theta function of a lattice is a function whose coefficients give the number of vectors of a given norm. One can associate to any...

(s)=\int _{0}^{\infty }{\bigl (}\theta (it)-1{\bigr )}t^{{\frac {s}{2}}-1}\,\mathrm {d} t,} in terms of Jacobi's theta function θ ( τ ) = ∑ n = − ∞ ∞ e π i...

_{0}^{\pi /2}{\frac {1}{({\sqrt[{z}]{\sin \theta }}+{\sqrt[{z}]{\cos \theta }})^{2z}}}\,d\theta } The beta function can be written as an infinite sum B ( x...

= ( θ − θ ^ ) 2 , {\displaystyle L(\theta ,{\hat {\theta }})=(\theta -{\hat {\theta }})^{2},} the risk function becomes the mean squared error of the...

Riemann–Siegel theta function and the Riemann zeta function by Z ( t ) = e i θ ( t ) ζ ( 1 2 + i t ) . {\displaystyle Z(t)=e^{i\theta (t)}\zeta \left({\frac...

{\sin ^{4}(\theta )}{\theta ^{4}}}\,d\theta ={\frac {2\pi }{3}}.} The following improper integral involves the (not normalized) sinc function: ∫ 0 ∞ d x...

)} . An example is the Jacobi theta function θ ( z , τ ) = ∑ n = − ∞ ∞ e 2 π i n z   +   π i n 2 τ {\displaystyle \theta (z,\tau )=\sum _{n=-\infty }^{\infty...

as Lovász theta function and is commonly denoted by ϑ ( G ) {\displaystyle \vartheta (G)} , using a script form of the Greek letter theta to contrast...

such as the Ramanujan prime, the Ramanujan theta function, partition formulae and mock theta functions, have opened entire new areas of work and inspired...

comparison, the generating function of the regular partition numbers p(n) has this identity with respect to the theta function: ∑ n = 0 ∞ p ( n ) x n =...

the sum of triangular numbers are connected to theta functions, in particular the Ramanujan theta function. The number of line segments between closest...

{\displaystyle X\sim \Gamma (\alpha ,\theta )\equiv \operatorname {Gamma} (\alpha ,\theta )} The probability density function using the shape-scale parametrization...

representation along with the residue theorem. A second proof uses a theta function identity, or equivalently Poisson summation. These proofs are analogous...

y^{2}=-q{\sqrt {q}}} . The Jacobi Triple Product also allows the Jacobi theta function to be written as an infinite product as follows: Let x = e i π τ {\displaystyle...