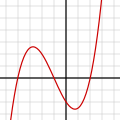
In mathematics, the Weierstrass function, named after its discoverer, Karl Weierstrass, is an example of a real-valued function that is continuous everywhere...

mathematics, the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named...

mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class...

In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on a closed interval [a, b] can be uniformly...

the Bolzano–Weierstrass theorem, and used the latter to study the properties of continuous functions on closed bounded intervals. Weierstrass was born into...

ellipse. Important elliptic functions are Jacobi elliptic functions and the Weierstrass ℘ {\displaystyle \wp } -function. Further development of this...

Weierstrass function, a function that is continuous everywhere but differentiable nowhere. The sum of a differentiable function and the Weierstrass function...

mathematics, the Weierstrass transform of a function f : R → R {\displaystyle f:\mathbb {R} \to \mathbb {R} } , named after Karl Weierstrass, is a "smoothed"...

{1}{n}}\right)^{z}}\right]} is an entire function, converging for every complex number z. The definition for the gamma function due to Weierstrass is also valid for all...

derivatives at all rational numbers. Dyadic transformation Weierstrass function, a function that is continuous everywhere but differentiable nowhere. Vestrup...

is continuous everywhere but differentiable nowhere is the Weierstrass function. A function f {\textstyle f} is said to be continuously differentiable...

functions: The inverses of elliptic integrals; used to model double-periodic phenomena. Jacobi's elliptic functions Weierstrass's elliptic functions Lemniscate...

drawing a tangent line to any point is impossible. Unlike the earlier Weierstrass function where the proof was purely analytical, the Koch snowflake was created...

numbers). The Weierstrass functions are doubly periodic; that is, they are periodic with respect to a lattice Λ; in essence, the Weierstrass functions are naturally...

particularly in the field of complex analysis, the Weierstrass factorization theorem asserts that every entire function can be represented as a (possibly infinite)...

associated with complex numbers include Euler, Gauss, Riemann, Cauchy, Weierstrass, and many more in the 20th century. Complex analysis, in particular the...

the Weierstrass sigma function, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ℘ function. Bloch's...

substitutions introduced by Weierstrass to integrate rational functions of sine, cosine.) Two decades later, James Stewart mentioned Weierstrass when discussing the...

Riemann function, on which the Weierstrass function has been based on. This disambiguation page lists articles associated with the title Riemann function. If...

quotients of the above four theta functions, and could have been used by him to construct Weierstrass's elliptic functions also, since ℘ ( z ; τ ) = − ( log...

analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions...

function. In particular, the function could be nowhere differentiable. (For example, f (x) could be a Weierstrass function.) The convergence of both series...

continuous function on a closed and bounded set obtains its extreme values The Weierstrass–Casorati theorem describes the behavior of holomorphic functions near...

the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R , {\displaystyle f\colon U\to \mathbb...

theorem Weierstrass coordinates Weierstrass's elliptic functions Weierstrass equation Weierstrass factorization theorem Weierstrass function Weierstrass functions...

nowhere. This example is now known as the Weierstrass function. In 1931, Stefan Banach proved that the set of functions that have a derivative at some point...

analysis, a branch of mathematics, the Casorati–Weierstrass theorem describes the behaviour of holomorphic functions near their essential singularities. It is...

shows uniformly continuous functions are not always differentiable. Despite being nowhere differentiable, the Weierstrass function is uniformly continuous...

(1964), Elements of real analysis, pp. 315–316 Weierstrass, Karl (1841). "Darstellung einer analytischen Function einer complexen Veränderlichen, deren absoluter...

In mathematics, the Weierstrass M-test is a test for determining whether an infinite series of functions converges uniformly and absolutely. It applies...