also co-invented the Berlekamp–Rabin algorithm, Berlekamp–Zassenhaus algorithm, and the Berlekamp–Van Lint–Seidel graph. Berlekamp had also been active...

In number theory, Berlekamp's root finding algorithm, also called the Berlekamp–Rabin algorithm, is the probabilistic method of finding roots of polynomials...

1987, Rabin, together with Richard Karp, created one of the most well-known efficient string search algorithms, the Rabin–Karp string search algorithm, known...

The Miller–Rabin primality test or Rabin–Miller primality test is a probabilistic primality test: an algorithm which determines whether a given number...

finding square roots modulo prime numbers. In 1970, Elwyn Berlekamp introduced a randomized algorithm for efficiently computing the roots of a polynomial over...

The Tonelli–Shanks algorithm (referred to by Shanks as the RESSOL algorithm) is used in modular arithmetic to solve for r in a congruence of the form r2...

In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking...

modulo a prime number Berlekamp's root finding algorithm Cipolla's algorithm Tonelli–Shanks algorithm Multiplication algorithms: fast multiplication of...

Euclidean algorithm also has other applications in error-correcting codes; for example, it can be used as an alternative to the Berlekamp–Massey algorithm for...

The Karatsuba algorithm is a fast multiplication algorithm for integers. It was discovered by Anatoly Karatsuba in 1960 and published in 1962. It is a...

The binary GCD algorithm, also known as Stein's algorithm or the binary Euclidean algorithm, is an algorithm that computes the greatest common divisor...

discovery of the Solovay–Strassen and Miller–Rabin algorithms put PRIMES in coRP. In 1992, the Adleman–Huang algorithm reduced the complexity to ⁠ Z P P = R...

efficient non-quantum integer factorization algorithm is known. However, it has not been proven that such an algorithm does not exist. The presumed difficulty...

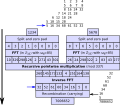
The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen...

A division algorithm is an algorithm which, given two integers N and D (respectively the numerator and the denominator), computes their quotient and/or...

Lenstra–Lenstra–Lovász (LLL) lattice basis reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and...

been largely superseded by the Baillie–PSW primality test and the Miller–Rabin primality test, but has great historical importance in showing the practical...

multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are more efficient...

theory, Williams's p + 1 algorithm is an integer factorization algorithm, one of the family of algebraic-group factorisation algorithms. It was invented by...

theory, the Pohlig–Hellman algorithm, sometimes credited as the Silver–Pohlig–Hellman algorithm, is a special-purpose algorithm for computing discrete logarithms...

ancient Egypt the concept of base 2 did not exist, the algorithm is essentially the same algorithm as long multiplication after the multiplier and multiplicand...

and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common...

Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor...

Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975. It uses only a small amount of space, and...

In computational number theory, the index calculus algorithm is a probabilistic algorithm for computing discrete logarithms. Dedicated to the discrete...

modular multiplicative inverse d of b modulo m using the extended Euclidean algorithm. That is: c = be mod m = d−e mod m, where e < 0 and b ⋅ d ≡ 1 (mod m)...

Pollard's rho algorithm for logarithms is an algorithm introduced by John Pollard in 1978 to solve the discrete logarithm problem, analogous to Pollard's...

is Berlekamp's algorithm, which combines stages 2 and 3. Berlekamp's algorithm is historically important as being the first factorization algorithm which...

y {\displaystyle y} and k {\displaystyle k} be non-negative integers. Algorithms that compute (the decimal representation of) y {\displaystyle {\sqrt {y}}}...

(also Dixon's random squares method or Dixon's algorithm) is a general-purpose integer factorization algorithm; it is the prototypical factor base method...