analysis, elliptic functions are special kinds of meromorphic functions, that satisfy two periodicity conditions. They are named elliptic functions because...

Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions is also...

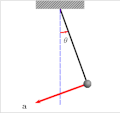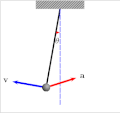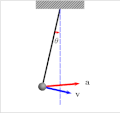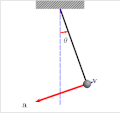
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum, as...

In mathematics, the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli. They were first studied...

In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied...

mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point O. An elliptic curve is defined...

In mathematics Abel elliptic functions are a special kind of elliptic functions, that were established by the Norwegian mathematician Niels Henrik Abel...

upper half space. The most common form of theta function is that occurring in the theory of elliptic functions. With respect to one of the complex variables...

sections of a line bundle on the moduli stack of elliptic curves. A modular function is a function that is invariant with respect to the modular group...

filter becomes a Butterworth filter. The gain of a lowpass elliptic filter as a function of angular frequency ω is given by: G n ( ω ) = 1 1 + ϵ 2 R...

mathematics, the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named for...

Elliptic functions: The inverses of elliptic integrals; used to model double-periodic phenomena. Jacobi's elliptic functions Weierstrass's elliptic functions...

global L-function; this would be a vast generalisation of the Taniyama-Weil conjecture, itself an important result in number theory. For an elliptic curve...

the elliptic curve y 2 = 4 x 3 − g 2 ( τ ) x − g 3 ( τ ) {\displaystyle y^{2}=4x^{3}-g_{2}(\tau )x-g_{3}(\tau )} (see Weierstrass elliptic functions). Note...

mathematics, the elliptic gamma function is a generalization of the q-gamma function, which is itself the q-analog of the ordinary gamma function. It is closely...

function is an element of the function field of such a curve, or of the Jacobian variety on the curve; these two concepts are identical for elliptic functions...

In mathematics, the Dixon elliptic functions sm and cm are two elliptic functions (doubly periodic meromorphic functions on the complex plane) that map...

Weierstrass sigma function, related to elliptic functions Rado's sigma function, see busy beaver See also sigmoid function. This disambiguation page lists mathematics...

In mathematics, the half-period ratio τ of an elliptic function is the ratio τ = ω 2 ω 1 {\displaystyle \tau ={\frac {\omega _{2}}{\omega _{1}}}} of the...

square of the elliptic modulus, that is, λ ( τ ) = k 2 ( τ ) {\displaystyle \lambda (\tau )=k^{2}(\tau )} . In terms of the Dedekind eta function η ( τ ) {\displaystyle...

Weierstrass zeta function was called an integral of the second kind in elliptic function theory; it is a logarithmic derivative of a theta function, and therefore...

was a German mathematician who made fundamental contributions to elliptic functions, dynamics, differential equations, determinants and number theory...

Spirograph (special case of the hypotrochoid) Jacobi's elliptic functions Weierstrass's elliptic function Formulae are given as Taylor series or derived from...

forms. In particular the modular discriminant of the Weierstrass elliptic function with ω 2 = τ ω 1 {\displaystyle \omega _{2}=\tau \omega _{1}} can...

specifically the theory of elliptic functions, the nome is a special function that belongs to the non-elementary functions. This function is of great importance...

solution. The Jacobian elliptic function that expresses the position of a pendulum as a function of time is a doubly periodic function with a real period...

mathematics the elliptic rational functions are a sequence of rational functions with real coefficients. Elliptic rational functions are extensively used...

cryptography, the Elliptic Curve Digital Signature Algorithm (ECDSA) offers a variant of the Digital Signature Algorithm (DSA) which uses elliptic-curve cryptography...

theory of elliptic curves E that have an endomorphism ring larger than the integers. Put another way, it contains the theory of elliptic functions with extra...

discovered automorphic forms as generalizations of trigonometric and elliptic functions. Through the Langlands conjectures, automorphic forms play an important...