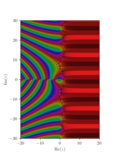
mathematics the elliptic rational functions are a sequence of rational functions with real coefficients. Elliptic rational functions are extensively used...

an elliptic filter will coincide with the poles of the elliptic rational function, which are derived in the article on elliptic rational functions. The...

In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied...

analysis, elliptic functions are special kinds of meromorphic functions, that satisfy two periodicity conditions. They are named elliptic functions because...

Weierstrass's elliptic functions Lemniscate elliptic functions Theta functions Neville theta functions Modular lambda function Closely related are the...

follows naturally from a curious property of Weierstrass's elliptic functions. These functions and their first derivative are related by the formula ℘ ′...

Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions is also...

In mathematics, the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli. They were first studied...

upper half space. The most common form of theta function is that occurring in the theory of elliptic functions. With respect to one of the complex variables...

number field K, the Hasse–Weil zeta function is conjecturally related to the group of rational points of the elliptic curve over K by the Birch and Swinnerton-Dyer...

numerators and denominators for constructing all the rational functions which are really functions on the underlying projective space P(V). One might ask...

Birch–Swinnerton-Dyer conjecture) describes the set of rational solutions to equations defining an elliptic curve. It is an open problem in the field of number...

the rank of an elliptic curve is the rational Mordell–Weil rank of an elliptic curve E {\displaystyle E} defined over the field of rational numbers or more...

applies to an elliptic curve E, and the problem it attempts to solve is the prediction of the rank of the elliptic curve over the rational numbers (or another...

is known, at least when A is an elliptic curve. The question of the rank is thought to be bound up with L-functions (see below). The torsor theory here...

Because they have an odd degree, normal quintic functions appear similar to normal cubic functions when graphed, except they may possess one additional...

constant. The elliptic functions are such functions. ("Incommensurate" in this context means not real multiples of each other.) Periodic functions can take...

polynomial, rational, trigonometric, hyperbolic, and exponential functions, and their inverses (e.g., arcsin, log, or x1/n). All elementary functions are continuous...

modeling), polynomial functions and rational functions are sometimes used as an empirical technique for curve fitting. A polynomial function is one that has...

filter is named after Wilhelm Cauer and the transfer function is based on elliptic rational functions. Cauer-type filters use generalized continued fractions...

particular the subfield of algebraic geometry, a rational map or rational mapping is a kind of partial function between algebraic varieties. This article uses...

In mathematics, an elliptic hypergeometric series is a series Σcn such that the ratio cn/cn−1 is an elliptic function of n, analogous to generalized hypergeometric...

asserts that every elliptic curve defined over the rational numbers is modular. In the 1950s and 1960s a connection between elliptic curves and modular...

)}=0,\quad j(i)=1728=12^{3}.} Rational functions of j {\displaystyle j} are modular, and in fact give all modular functions of weight 0. Classically, the...

field of rational numbers, the field of real numbers and the field of complex numbers. Many other fields, such as fields of rational functions, algebraic...

circuits. Cauer used elliptic rational functions to produce approximations to ideal filters. A special case of elliptic rational functions is the Chebyshev...

the lemniscate leads to elliptic integrals, as was discovered in the eighteenth century. Around 1800, the elliptic functions inverting those integrals...

determining the type of a singular fiber in an elliptic pencil", in Birch, B.J.; Kuyk, W. (eds.), Modular Functions of One Variable IV, Lecture Notes in Mathematics...

was a German mathematician who made fundamental contributions to elliptic functions, dynamics, differential equations, determinants and number theory...

known as the modularity theorem), which states that every elliptic curve over the rational numbers is modular. This conjecture became central to modern...